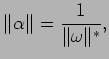Proof.
Following Gromov's notation in [
Gro99, Theorem 4.36], we let
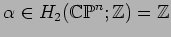 |
(5.1) |
be the positive generator in homology, and let
be the dual generator in cohomology. Then the cup power
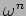
is
a generator of
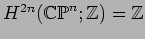
. Let
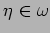
be a
closed differential 2-form. Since wedge product
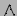
in
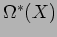
descends to cup product in
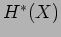
, we have
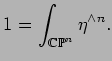 |
(5.2) |
Now let
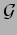
be a metric on
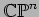
. Recall that the pointwise
comass norm for a simple
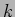
-form coincides with the natural Euclidean
norm on
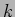
-forms associated with
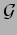
. In general, the comass
is defined as follows.
Definition 5.2
The comass of an exterior
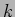
-form is its maximal value on a
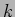
-tuple
of unit vectors.
The comass norm of a differential 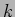 -form is, by definition, the
supremum of the pointwise comass norms. Then by the Wirtinger
inequality
we obtain
-form is, by definition, the
supremum of the pointwise comass norms. Then by the Wirtinger
inequality
we obtain
where
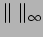
is the comass norm
on
forms. See [
Gro99, Remark 4.37] for a discussion of the constant
in the context of the Wirtinger inequality
. A more detailed discussion appears in
[
Ka07, Section 13.1].
The infimum of (5.3) over all
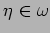 gives
gives
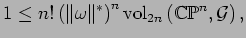 |
(5.4) |
where
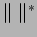
is the comass norm in cohomology. Denote by
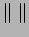
the stable norm
in homology. Recall that the
normed lattices
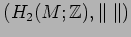
and
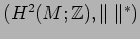
are
dual to each other [
Fed69]. Therefore the class
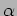
of (
5.1) satisfies
and hence
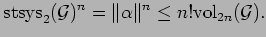 |
(5.5) |
Equality is attained by the two-point homogeneous Fubini-Study metric,
since the standard line
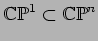
is calibrated by the
Fubini-Study Kahler
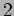
-form, which satisfies equality in the
Wirtinger inequality at every point.
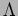
![]() -form is, by definition, the
supremum of the pointwise comass norms. Then by the Wirtinger
inequality
we obtain
-form is, by definition, the
supremum of the pointwise comass norms. Then by the Wirtinger
inequality
we obtain
![]() gives
gives