



Next: Bibliography
Up: A sixty second introduction
Previous: Gromov's inequality for complex
Contents
There is a number of inequalities in the systolic literature that
could be described as Gromov's inequality.
The deepest result in systolic geometry is Gromov's
inequality for the homotopy 1-systole of
essential manifolds. Gromov's original definition of an essential
manifold 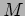 depends on the
choice of the coefficient ring
depends on the
choice of the coefficient ring 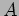 , taken to be
, taken to be
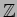 if
if 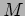 is
orientable, or
is
orientable, or
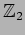 otherwise. We then have a nonzero fundamental
homology class
otherwise. We then have a nonzero fundamental
homology class
![$ [{M}]\in H_n({M},A)$](img71.png) .
.
Definition 6.1
A closed
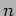
-dimensional manifold
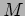
is called
essential if there exists a map from
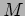
to a suitable
Eilenberg-MacLane space
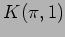
such that the induced homomorphism
maps the fundamental class
![$ [{M}]$](img75.png)
to a nonzero class in the
homology group
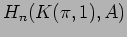
,
i.e.
![$ h([{M}])\not= 0$](img77.png)
.
A more general definition of an 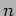 -essential space
-essential space 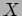 , in the
context of an arbitrary polyhedron
, in the
context of an arbitrary polyhedron 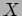 ,
can be defined in terms of arbitrary local coefficients.
,
can be defined in terms of arbitrary local coefficients.
The following theorem was proved
in [Gro83, Section 0] and [Gro83, Appendix 2, p. 139,
item  ].
].
In other words, the quotient
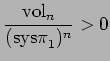 |
(6.2) |
is bounded away from zero for such polyhedra.
A summary of a proof appears in [Ka07, Section 12.2].




Next: Bibliography
Up: A sixty second introduction
Previous: Gromov's inequality for complex
Contents
Mikhail Katz
2007-09-19
![]() depends on the
choice of the coefficient ring
depends on the
choice of the coefficient ring ![]() , taken to be
, taken to be
![]() if
if ![]() is
orientable, or
is
orientable, or
![]() otherwise. We then have a nonzero fundamental
homology class
otherwise. We then have a nonzero fundamental
homology class
![]() .
.
![]() ].
].