



Next: Gromov's inequality for complex
Up: A sixty second introduction
Previous: Loewner's torus inequality
Contents
We recall the definition of the stable norm in the real homology of a
polyhedron 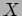 with a piecewise Riemannian metric, following
[BaK03,BaK04].
with a piecewise Riemannian metric, following
[BaK03,BaK04].
Definition 4.1
The stable norm
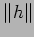
of
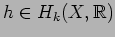
is the infimum of
the volumes
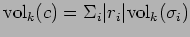 |
(4.1) |
over all real Lipschitz
cycles
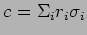
representing
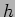
.
Note that 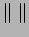 is indeed a norm, cf. [Fed74] and
[Gro99, 4.C].
is indeed a norm, cf. [Fed74] and
[Gro99, 4.C].
We denote by
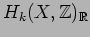 the image of
the image of
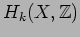 in
in
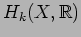 and by
and by
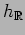 the image of
the image of
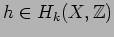 in
in
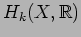 . Recall that
. Recall that
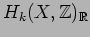 is a lattice in
is a lattice in
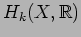 . Obviously
. Obviously
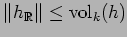 |
(4.2) |
for all
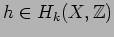 , where
, where
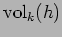 is the infimum of volumes
of all integral
is the infimum of volumes
of all integral 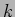 -cycles representing
-cycles representing 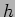 . Moreover, one
has
. Moreover, one
has
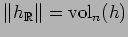 if
if
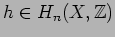 . H. Federer
[Fed74, 4.10, 5.8, 5.10] (see also [Gro99, 4.18 and 4.35])
investigated the relations between
. H. Federer
[Fed74, 4.10, 5.8, 5.10] (see also [Gro99, 4.18 and 4.35])
investigated the relations between
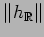 and
and
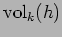 and
proved the following.
and
proved the following.
Proposition 4.2
If
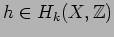 ,
,
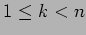 , then
, then
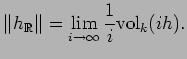 |
(4.3) |
Equation (4.3) is the origin of the term stable
norm for 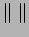 . The stable
. The stable 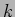 -systole of a
metric
-systole of a
metric
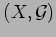 is defined by setting
is defined by setting
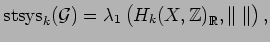 |
(4.4) |
where 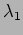 denotes the first successive minimum of the lattice
denotes the first successive minimum of the lattice
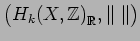 , i.e. the least
norm of a nonzero lattice element.
, i.e. the least
norm of a nonzero lattice element.




Next: Gromov's inequality for complex
Up: A sixty second introduction
Previous: Loewner's torus inequality
Contents
Mikhail Katz
2007-09-19
![]() with a piecewise Riemannian metric, following
[BaK03,BaK04].
with a piecewise Riemannian metric, following
[BaK03,BaK04].
![]() is indeed a norm, cf. [Fed74] and
[Gro99, 4.C].
is indeed a norm, cf. [Fed74] and
[Gro99, 4.C].
![]() the image of
the image of
![]() in
in
![]() and by
and by
![]() the image of
the image of
![]() in
in
![]() . Recall that
. Recall that
![]() is a lattice in
is a lattice in
![]() . Obviously
. Obviously
![]() . The stable
. The stable ![]() -systole of a
metric
-systole of a
metric
![]() is defined by setting
is defined by setting