



Next: Loewner's torus inequality
Up: A sixty second introduction
Previous: Isoperimetric inequality
Contents
In the 1950's, Charles Loewner's student P. M. Pu [Pu52] proved the
following theorem. Let
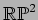 be the real projective plane endowed
with an arbitrary metric, i.e. an imbedding in some
be the real projective plane endowed
with an arbitrary metric, i.e. an imbedding in some
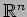 . Then
. Then
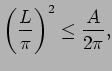 |
(2.1) |
where 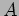 is its total area and
is its total area and 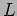 is the least length of a
non-contractible loop. This isosystolic inequality, or simply
systolic inequality for short, is also sharp, to the extent
that equality is attained precisely for a metric of constant Gaussian
curvature, namely antipodal quotient of a
round sphere.
In the systolic notation
where
is the least length of a
non-contractible loop. This isosystolic inequality, or simply
systolic inequality for short, is also sharp, to the extent
that equality is attained precisely for a metric of constant Gaussian
curvature, namely antipodal quotient of a
round sphere.
In the systolic notation
where 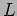 is replaced by
is replaced by 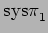 , Pu's inequality takes the following form:
, Pu's inequality takes the following form:
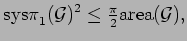 |
(2.2) |
for every metric
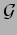 on
on
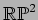 .
.
For a proof, see [Ka07, Section 6.5].
Pu's inequality can be generalized as follows.
Theorem 2.1
Every surface
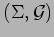 different from
different from 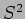 satisfies the
optimal bound (2.2), attained precisely when, on the one hand,
the surface
satisfies the
optimal bound (2.2), attained precisely when, on the one hand,
the surface 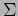 is a real projective plane, and on the other,
the metric
is a real projective plane, and on the other,
the metric
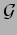 is of constant Gaussian
curvature.
is of constant Gaussian
curvature.
The extension to surfaces of nonpositive Euler characteristic follows
from Gromov's inequality (2.3) below (by comparing the
numerical values of the two constants). Namely, every aspherical
compact surface
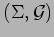 admits a metric ball
admits a metric ball
of radius
 which satisfies
[Gro83, Corollary 5.2.B]
which satisfies
[Gro83, Corollary 5.2.B]
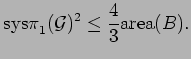 |
(2.3) |




Next: Loewner's torus inequality
Up: A sixty second introduction
Previous: Isoperimetric inequality
Contents
Mikhail Katz
2007-09-19
![]() be the real projective plane endowed
with an arbitrary metric, i.e. an imbedding in some
be the real projective plane endowed
with an arbitrary metric, i.e. an imbedding in some
![]() . Then
. Then
![]() admits a metric ball
admits a metric ball