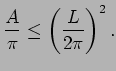Pu's inequality can be thought of as an ``opposite'' isoperimetric inequality, in the following precise sense.
The classical isoperimetric inequality in the plane is a relation
between two metric invariants: length 
of a simple closed curve in
the plane, and area 
of the region bounded by the curve. Namely,
every simple closed curve in the plane satisfies the inequality
