סוגיות
גאומטריות
בספרות חז"ל
בועז
צבאן, דוד
גרבר
המחלקה
למתמטיקה, אוניברסיטת
בר-אילן
הקדמה
במהלך
שנת ה'תשנ"ב
התחלנו מחקר
שמטרתו לימוד,
ניתוח וסיווג
כל הסוגיות
הנוגעות
לנושא המעגל
והעיגול
בתלמוד
ובמפרשיו
בצורה שיטתית
ואחידה[1].
אמנם מחקר זה
עדיין נמשך,
אולם נראה
שהגענו למקום
בו ראוי
להתבונן
לאחור ולסכם
את שנעשה עד
כה. המטרות
שהצבנו
בפנינו היו (בסדר
לוגי):
א. יצירת
בסיס מתמטי
אחיד לנושא
כולו.
ב. לימוד
הסוגיות
השונות
וזיהוי שורשן
המתמטי, המסתעף
מהבסיס
שיצרנו ב-(א).
ג. נסיון
להבין את דרכי
החשיבה של
חז"ל בנוגע לחלקים
המתמטיים של
הסוגיה, לאור
שיטות אנליזה מקובלות
במתמטיקה
ובדרכי חשיבה
אוניברסליות-לוגיות.
ד. הסקה
זהירה של
שיטות חדשות
בסוגיות, לאור
ההכללות
המתמטיות
הטבעיות.
ה. סיקול
ספיקות שעמדו
בפני מפרשים
בגשתם אל הסוגיות,
באמצעות כלים
מודרניים.
במאמר
זה נשלב את המסקנות
העולות
ממאמרינו
השונים
במסגרת אחידה,
לאור המטרות
דלעיל[2].
א.
בסיס מתמטי
אחיד
הבסיס
המתמטי נועד
לתת מיסוד לפן
המתמטי של הסוגיות,
שהוא חופשי
לחלוטין
מההקשר שבו
מופעלים
הכללים
השונים. בסיס
זה מהווה
מסגרת פורמלית
אחידה, ומכיל
את הוכחת
הכללים בהם
השתמשו האמוראים
בגשתם להבין
מאמר מתקופה
מוקדמת יותר:
תקופת התנאים
או תחילת
תקופת
האמוראים. העיסוק
בתחום עדין זה
דורש זהירות
מירבית, שאינה
אפשרית ללא
שליטה
ביסודות
המתמטיקה
והלוגיקה.
למשל, כאשר
חז"ל מחשבים
היקף של עיגול
שקוטרו ארבע
אמות (סוכה, דף
ז' ע"ב), הם
מציינים את
הכלל "כל שיש
בהיקפו שלשה
טפחים, יש בו רוחב
טפח". אולם, יש
להקשות על כך
מספר קושיות:
ראשית, הכלל
עוסק בטפחים,
ולא באמות.
שנית, הכלל מדבר
רק בעיגול
שרוחבו יחידה
אחת (טפח), ולא
ארבע יחידות
(אמות),
ושלישית, אין
הוא נותן דרך
להסיק את
ההיקף מהרוחב,
אלא את הרוחב
מההיקף! נדרש
לפיכך ניסוח
מתמטי של הכלל,
שחז"ל רק
נוקטים דוגמא
שלו:
1. כל
המעגלים דומים,
דהיינו: היחס
בין היקפיהם
שווה ליחס בין
קוטריהם [1,
הגדרה 1.2
ואקסיומה 1.3].
2. היקף
מעגל הוא 3
יחידות אם ורק
אם קוטרו הוא
יחידה אחת [1,
תוצאה 1.5].
גם
השימוש
בַּכְּלל - אין
הכוונה לכפול
את הקוטר (או
לחלק את
ההיקף) ב3-
בצורה פשוטה,
אלא להשתמש
בתורת
הפרופורציות [1,
הערות 1.6,1.8].
כללים
גאומטריים
אחרים של חז"ל
דורשים לא רק
ביסוס
אקסיומטי, אלא
אף הוכחה
מתמטית. כאלו
הם הטענה
שהיקף עיגול
החסום בריבוע
קטן ברבע
מהיקף הריבוע
(סוכה, דף ח' ע"א,
ועוד), שהיחס
בין אורך
אלכסון של ריבוע
לאורך צלעו
הוא ![]() בקירוב,
ועוד [1,
משפטים 1.9,1.11,1.13].
בקירוב,
ועוד [1,
משפטים 1.9,1.11,1.13].
חלק זה
של עבודתנו
הכרחי לשם
"בירור" החלק
המתמטי מתוך
הסוגיות
ומיסודו,
ומאוחר יותר -
לשם יצירת
האנלוגיות
וההכללות.
בסיס זה משמש
נקודת מוצא
לכל מאמרינו.
יש
לציין גישה
דומה אצל הרב
סתהון[3]
שחלקה אימצנו
ב [8]. בבואו
לפענח את
סוגיית "סוכה
העשויה
ככבשן", פותח
הרב סתהון
בהקדמות
מתמטיות
טהורות, הכוללות
את השיטות
הדרושות לו
לשם ביאור
הסוגיה. ברם,
יש לציין
שהדמיון
לעבודתנו הוא
רק בגישה
המבנית (של
הקדמת הדיון
המתמטי הבלתי
תלוי). ההבדל
המהותי הינו,
שהקדמות הרב
סתהון אינן מצויינות
בגמרא, וכן
אינן משמשות
אותו להכללה,
אלא לפתרון
סוגיה
ספציפית.
ב.
השורש המתמטי
של הסוגיה
בכל אחת
מהסוגיות
מופעלת
החוקיות
בהתאם להקשר
ההלכתי. בחלק
זה של העבודה
ניסינו, לאור
האמור בסעיף
הקודם, לברר
מהו החלק שאפשר
לנתק מההקשר
ההלכתי ולבסס
על הבסיס המתמטי
בלבד. אותו
חלק המהווה את
השלד המתמטי
של הסוגיה
אינו תלוי
בהלכה (כגון:
דיני סוכה, דיני
עירוב חצרות,
דיני הוצאה
מרשות לרשות
בשבת, וכו');
אינו תלוי
ביחידות שבהן
משתמשים (אמה,
טפח); ולא
בדמויות
הפועלות (רבי
יוחנן, מר קשישא,
רמי בר יחזקאל
ועוד). אנו
מעונינים רק
באותו חלק
אוניברסלי של
הסוגיה, החלק
שיהיה תקף גם
אם נדון בהלכה
אחרת, לשיטת
חכמים אחרים,
ביחידות
אחרות וכו'. כך
אפשר לזהות
שלד משותף עבור
סוגיות שונות.
למשל, החלק הראשון
של סוגיית
"סוכה העשויה
ככבשן" (סוכה,
דף ח' ע"א)
ו"חלון עגול"
(עירובין, דף
ע"ו) מבוסס על שלד
מתמטי שאפשר
למצותו
במשפטים
הבאים:
1. היקף
עיגול שקוטרו
4 יחידות, הוא 12
יחידות [1,
טענה 2.1].
2. היקף
ריבוע
שמימדיו 4
יחידות x 4
יחידות הוא 16
יחידות [1,
טענה 2.3].
3. עיגול
שהיקפו 16
יחידות לא
יכול לחסום
ריבוע שמימדיו
4 יחידות x 4
יחידות [1,
טענה 2.5].
4. היקף
עיגול החוסם
ריבוע
שמימדיו 4
יחידות x 4
יחידות הוא ![]() יחידות [1,
טענה 2.7].
יחידות [1,
טענה 2.7].
ההוכחות
לטענות אלו
בנויות כולן
על אדני הבסיס
שיצרנו בחלק
הקודם. בהמשך
משמש חלק זה
נקודת מוצא
לביצוע
השוואות בין-סוגייתיות,
ולהשלכות
מסוגיה אחת
לסוגיה אחרת.
ג.
שיחזור טעמים
אבודים
חלק זה
והחלק הבא
אחריו דרשו
מעט יותר
"אומץ". כאן
ניסינו לשחזר
את מהלך
החשיבה של
חז"ל במקרים
שבהם אין
הכתוב מוסר
לנו מידע זה.
מסתבר שאפשר
ליישם מתודות
היסק
אוניברסליות
לקבלת
המסקנות המתמטיות
המובאות
בתלמוד.
1. מהלך
תמוה בסוגיה
בסוגיות
"סוכה עגולה"
ו"חלון עגול"
ישנו חלק
שנראה תמוה או
מיותר במבט
ראשוני: בכל
הסוגיה מנסה
הגמרא למצוא
את שיעורי
המעגל שחוסם
ריבוע 4x4, והנה
בטיעון זה
נראה שהגמרא
מציעה שהיקף
המעגל יהיה
כהיקף הריבוע.
לא ברור כיצד
הצעה זו מקרבת
אותנו אל
המטרה; ויתר
על כן, לא ברור במבט
ראשוני מנין
מסיקה הגמרא,
שהיקף 16 עבור המעגל
אינו מספיק
כדי לחסום את
הריבוע, שהרי
חישוב ההיקף
של עיגול חוסם
מבוצע רק
בהמשך הסוגיה.
ספיקות אלו
עלולים
להוביל את התלמיד
הנבוך למסקנה,
שהחלק שמדבר
על היקף 16, והחלק
הבא אחריו - של
חישוב ההיקף -
הם חלקים בלתי
תלויים
ש"נתפרו" על
ידי עורכי
הגמרא בצורה מלאכותית,
ולכן אין
לקראם ברצף.
במאמרנו [1, עמ' 111,
תוצאה 2.5] מצאנו
פתרון
לתעלומה זו:
הצעת היקף 16
ופסילתה
מסתמכים על
עקרון פרימיטיבי
יותר מבחינה
גאומטרית,
והוא שהמיתר
קצר מהקשת הנשענת
עליו. יוצא, אם
כן, שבעריכת
הסוגיה היתה התחשבות
בשיקול מתמטי!
נקודה
נוספת שיש
לציין היא,
שבהסבר היסק
זה (ראה שם)
השתמשנו
בעקרון
לוגי-אוניברסלי,
שהוא שימושי
מאד במתמטיקה:
הוכחה בדרך
השלילה עם הנחות
מקילות, שבה
מגיעים
לסתירה. עקרון
זה מזכיר את
עקרון ההיסק
התורני "קל
וחומר".
2. כשלון
כפול
במקום
אחר הסברנו את
דרך ההיסק של
חז"ל באמצעות
עקרון ערך
הביניים
מהמתמטיקה,
המסייע במציאת
פתרון נכון
מתוך שני
נסיונות
שגויים במכוון,
שהשגיאות בהם
הן בעלות אופי
שונה ("יותר
מדי" לעומת
"פחות מדי"):
למציאת צורת
הים שעשה
שלמה, מנסה
הגמרא (בהתבסס
על הפסוק במל"א,
ז' כ"ג) צורה
בעלת נפח גדול
מהדרוש (תיבה), ולאחר
מכן צורה בעלת
נפח קטן
מהדרוש (גליל),
וכך מגיעה
לצורה בעלת
הנפח הדרוש,
שהיא צורת ביניים.
הצעה זו טומנת
בחובה רעיון
מהותי: אין
מדובר בניסוי
וטעיה גרידא,
אלא בשגיאה
מכוונת,
המוכיחה שיש
פתרון
ומסייעת לתחם
אותו, ובסופו
של דבר לגלותו
[1, "מציאת
צורת הים שעשה
שלמה", עמוד 117].
3. משנה
סתומה
משנת
"עמוד שהוא
מוטל לאויר"
(אהלות פרק י"ב
משנה ז') עוסקת
בעמוד עגול
המונח על הארץ
לאורכו, כך
שנוצר חלל בין
צידי העמוד
לארץ (ציור 1).
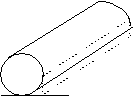
ציור 1
נשאלת
השאלה, מה
צריך להיות
היקף העמוד
כדי שאפשר
יהיה להכניס
בחלל זה ריבוע
שמימדיו טפח על
טפח (ציור 2).
![]()
ציור 2
תשובת
המשנה - 24 טפחים - היתה
מקור לתהיות
רבות של
חכמים,
ראשונים ואחרונים,
ולא נמצא לה
הסבר מניח את
הדעת[4].
ב [8] אנו
מביאים הסבר
מלא לסוגיה,
המנסֶה לשחזר
את שיקולי
התנא, ברוח
הסברו של
גינצבורג [17]:
התנא השתמש
בקירוב הפשוט
ביותר מתוך
סדרת קירובים
הולכים
ומדוייקים,
וזאת כדי לקרב
את ההבנה אל
התלמידים
(הגישה לקרב
את ההבנה אל התלמידים
מובאת כבר
בשו"ת התשב"ץ[5]
חלק א' סימן
קס"ה). סדרת
הקירובים
מושגת על ידי שימוש
בשיטה שתוארה
על יד הרב
סתהון (ראה
הערה 3): שיטת
האינטרפולציה
הלינארית, שבה
מחושב ערכה של
פונקציה
סתומה על ידי
קירוב לינארי[6].
ד.
חידושים
והכללות
עצם
הכתיבה
המתמטית
אומרת
"הכלילני".
בכל מקרה שבו
אפשר לזהות
שורש משותף
לסוגיות
שונות, אפשר
לנסות ליישם
את המסקנות
והפירושים
שבסוגיה אחת -
עבור הסוגיה
האחרת[7].
פשטות הכתיבה
המתמטית אינה
דורשת מאמץ רב
בבדיקת
אפשרויות אלה,
ולשמחתנו
גילינו, בעקבות
ההכללות,
הצעות לשיטות
חדשות בהסבר
הסוגיות;
שיטות שלא
מצאנו
במפרשים[8].
נציג להלן
מספר דוגמאות.
1. סוכה
אצל חלון
כאמור
לעיל (פרק ב'),
סוגיית "חלון
עגול" אנלוגית
ברובה
לסוגיית
"סוכה העשויה
ככבשן". האנלוגיה
אינה רק
במבנה, אלא אף
בשיעורים:
בשתי הסוגיות
נדרש שהיקף
המעגל (הסוכה
או החלון)
יהיה 24 יחידות.
ב [2] ניצלנו
עובדה זו לקבל
שיטות חדשות
בהסבר סוגיית
"סוכה העשויה
ככבשן".
לדוגמא:
פירושיהם של
הריטב"א
והגר"א,
שנכתבו
לסוגיית
"חלון עגול"
(ולא נזכרו
בסוגיה דנן)
נוצלו לקבלת
הסברים חדשים
בסוגיית
"סוכה העשויה
ככבשן" [2, עמ' 127-128].
2. סוכה
וחלון אצל
כוורת
בסוגיות
"סוכה העשויה
ככבשן", "חלון
עגול" ו"כוורת"
[2; 4; 6] נעשה
נסיון לחשב
היקף מעגל
החוסם ריבוע.
בכל המקרים,
תוצאת החישוב
קטנה מהשיעור
הנדרש על פי
ההלכה. מסתבר[ASD1], כי כל
אחת מהסוגיות
זכתה לטיפול
נפרד בידי
המפרשים.
למשל, שיטת
רבינו חננאל
ב"כוורת". לפי
שיטה זו, הפער
בין העובי
ההלכתי לבין
העובי המחושב בסוגיית
"כוורת" נובע
מכך שההלכה
מדברת בקוטר
הכוורת כשהוא
נמדד מבחוץ,
כלומר יחד עם
עובי דפנות
הכוורת, בעוד
שהחישוב
הגיאומטרי
מדבר על הקוטר
הפנימי, בלא
הדפנות. שיטה
זו אינה
מופיעה
בהתייחסות
לסוגיות
"סוכה העשויה
ככבשן"
ו"חלון עגול",
למרות שישומה
שם נראה טבעי
ועשוי לפתור
מספר בעיות
(ראה [4, עמ' 59,
הערה 17, וכן
"שיטת ר"ח" עמ'
63-62]; [2, עמ' 126, הערה 14,
ועמ' 127 סעיף 2]).
שיטה זו
(התחשבות
בעובי הדופן)
היא למעשה
יישום אחת
ההצעות
שמביאה הגמרא
בסוגיית "ים
שעשה שלמה"
בעירובין דף
י"ד ע"א,
האומרת כי
היקף המיכל העגול
נמדד מבפנים,
בעוד שהקוטר -
מבחוץ, ועיין [10].
נעיר
שגישת הלימוד
מתוך הכללה
היתה הקו המנחה
ב [4], שם אנו
לומדים את
סוגיית
"כוורת" מתוך
השוואה
לסוגיות
האחרות. למשל, ההסבר
שמביא רש"י
לפער בין
ההיקף ההלכתי
לגאומטרי -
שיש כאן
אי-דיוק קטן
ולחומרא -
אנלוגי להסבר
שמביאה הגמרא
עצמה בסוגיית
"סוכה העשויה
ככבשן" [4, עמ' 60].
וכן הסברו של
הרמב"ם
בפירושו
לתלמוד[9],
שההבדל נובע
משום חשש
לדיוקו של ![]() , לו אנו
מביאים
סימוכין
מסוגיה אחרת
העוסקת
בעניני שבת, ובה
יש הוספה על
השיעור משום
חשש לדיוקו,
ודומה לזה
יישומנו של
שיטת הרב
סתהון [4, עמ' 68][10].
, לו אנו
מביאים
סימוכין
מסוגיה אחרת
העוסקת
בעניני שבת, ובה
יש הוספה על
השיעור משום
חשש לדיוקו,
ודומה לזה
יישומנו של
שיטת הרב
סתהון [4, עמ' 68][10].
3. סוכה
אצל עמוד
בסוף
חלק ג' לעיל
הצגנו הסבר
למשנת "עמוד
שהוא מוטל
לאויר". אלמלא
שיטת הלימוד
מתוך אנלוגיה
והכללה, לא
היינו מגיעים
להסבר זה:
שיטת הרב
סתהון מוצגת,
במקור, בהקשר
של "סוכה
העשויה
ככבשן", ואין
אפילו רמז
לאפשרות
ליישמה למשנת
"עמוד שהוא
מוטל לאויר".
אלמלא שיטת
הלימוד מתוך
הכללה, היתה
משנה זו נשארת
סתומה כשהיתה
[8].
ה.
סיקול ספיקות
מבחינה
לוגית, יש
לראות חטיבה
זו של העבודה
כבלתי-תלויה
בקודמותיה,
למרות שמבחינה
כרונולוגית -
היא נדרשת
להן. ההבדל
העקרוני הוא
שבחטיבה זו -
בניגוד
לקודמותיה -
לא ניסינו
להבין את דברי
חז"ל
והמפרשים
מתוך נקודת הראות
של תקופתם,
אלא בהשתמש
בכלים החזקים
שמספקת לנו
המתמטיקה
המודרנית.
המטרה
המוצהרת -
סיקול ספיקות
הקדמונים -
היא ש"קידשה"
אמצעים אלו.
התוצאות
שהתקבלו
ממחישות כמה
עגמת נפש אפשר
לחסוך מאיש
ההלכה בעולם
המודרני, וזאת
בעזרת שימוש
בכלים
מתמטיים
מוכרים.
לדוגמא:
1. הוכחת
ראב"ח
ב"חיבור
המשיחה
והתשבורת" [15,
שער שני, סעיף 95
עמ' 61], מביא
ראב"ח[11]
הוכחה נפלאה
המקשרת בין
שטח עיגול
להיקפו (שטח
עיגול שווה
למחצית מכפלת
היקפו
בקוטרו).
ברם, הוכחה
זו, כיון
שהובאה עבור
אנשים חסרי
רקע מתמטי, לא
הכילה את
הפרטים
הדרושים לשם
ביסוסה
המתמטי[12].
משום כך, נוצר
חוסר אמון אצל
חכמינו בנוגע
לנכונות
ההוכחה, עד
כדי הטלת ספק
בנכונות
הנוסחה עצמה
ומשום כך - ויתור על
שיטות
מסוימות
בהסבר
הסוגיות
הרלוונטיות
בתלמוד. כך
למשל מובא
בשו"ת "חתם
סופר"[13]:
והנה
בתוספות סוכה
ח' ע"א כתב,
שאין ללמוד
חוט המקיף
מגוף הקרקע,
כי על ענין זה
על זה ע"ט (עיין
שם?) חבל (אבל?)
איך אפשר
להכחיש החוש.
וראיתי
ב"חוות יאיר"
סימן קע"ב דף
קס"ד ע"א, שהרבה
להקשות על הך
כללא של
תוספות, מ"ש
מגוף הקרקע על
ידי חתיכת
החוטין, וכל
דבריו שם
נכונים לכאורה,
עיין שם היטב.
על כן לא נראה
לי להעמיד יסוד
כלל על הך
כללא דגוף
הקרקע שכתבו
תוספות, ונראה
לי שכל דבריהם
שבפרק ערבי פסחים
(דף ק"ט) הוא על
יסוד דחוט
המקיף המרובע
הוא יתר רביע
על חוט המקיף
העיגול.
בנספח ל [1]
הבאנו, בפעם
הראשונה,
הוכחה מתמטית
מלאה ומפורטת
לנכונות שיטת
ההוכחה של
ראב"ח[14].
ב [11] אנו
מביאים דרכי
הוכחה שונות,
שייתכן מאד שווריאציה
של אחת מהן
שימשה כבסיס
מתמטי
להוכחתו של
ראב"ח[15].
2. נפחי
מקוואות
מיוחדים
בשו"ת
התשב"ץ[16]
ישנם מספר
סימנים שדנים
בחישוב נפח של
כדור קטום
(לשם קביעת
כשרותו של
מקוה בעל צורה
זו). מוזכרות
שם מספר
נוסחאות שלא
ברור כלל אם
הן נכונות ומה
מקורן. ב [1, עמ' 118 -
120], אנו מפתחים
את הנוסחאות
המדויקות.
מסתבר שאף אחת
מהנוסחאות
שהובאו בתשב"ץ
אינה נכונה;
אולם אחת מהן
מהווה קירוב
לינארי
לנוסחה
שמצאנו. כיון
שאי-הדיוק
עלול להוביל
לקולא, אין
לאיש ההלכה
ברירה מעשית
אלא להשתמש
בנוסחה
המדויקת
שמצאנו [1,
הערה 58].
3. הוצאת
שורשים
אחת
השיטות
הקדומות
לחישוב שורש
בקירוב - למשל
כדי למצוא את
אלכסונו של ריבוע
- היא
האינטרפולציה
הלינארית
(שנזכרה בסוף
פרק ג' לעיל).
בעזרת הכלים
של החשבון
הדיפרנציאלי,
אנו מסוגלים
להעריך את טיב
הקירוב, כך שיוכל
המשתמש
להשתמש
בקירוב זה תוך
בקרת השגיאה
והימנעות
מאי-דיוקים
לקולא [8].
4.
גיאומטריה
ניסית בבית
המקדש
ב [19]
הציע מונק
שיטה אמיצה
להסבר הפסוק
המפורסם בנוגע
לים שעשה שלמה
(מל"א, ז' כ"ג),
שבו נאמר כי
היקפו של
המיכל - שהיה
עגול - הוא 30
אמות, ורוחבו
היה 10 אמות.
מונק מציע,
שהיחס בין
היקף המיכל
לקוטרו בתחום
בית המקדש היה
באמת 3 ולא p
(...3.14). הוא מתרץ
זאת במציאות
הניסית שהיתה
בבית המקדש,
שבה לא
התקיימו
החוקים
הגיאומטריים
ה"סטנדרטיים".
כנגד שיטה זו
יוצא אסא כשר [18],
ומנסה לקעקע
אותה עד היסוד
כ"חסרת שחר".
הבעיה של מונק
היתה שחסר לו
הידע, שנפוץ
היום הרבה יותר
מבימיו, בנוגע
לגאומטריות
אלטרנטיביות
ומודלים
לוגיים. ב [7]
אנו מראים,
שטענות כשר
אינן נכונות,
כיון שמבחינה
לוגית יש
לדברי מונק
מקום להתגדר
בהם: קיימים
מודלים
מתמטיים שבהם
היחס בין היקף
עיגול לקוטרו
יכול להיות
בדיוק 3. ואולי
בעידן
התיאוריות
האלטרנטיביות
כתורות
היחסות ותורת
הקוואנטים,
נהיה פתוחים
יותר לקבל
רעיונות
חדשניים כאלה.
5. המטרה
מקדשת את
האמצעים
על
הלגיטימציה
לשימוש בכלים
מתמטיים
מודרניים
בנוגע לשאלות
הלכתיות נוכל
ללמוד מהמקורות
שלנו.
כנגד
הטוענים
שההלכה אינה
צריכה
למתמטיקה הכללית,
נביא את דברי
ראב"ח [15,
הקדמת המחבר]:
וכתיב
"אני ה' מלמדך
להועיל
מדריכך בדרך
תלך", מלמדך כל
דבר שהוא
מועיל לך
ומדריכך בדרך
תלך והוא דרך
התורה. ואתה
דורש מן הפסוק
הזה, כי כל עסק
וכל חכמה שהיא
מועילה לאדם
בדרכי החיים ובדבר
מצוה ראוי לו
ללמדה
ולהתעסק בה.
וראיתי חכמת
המנין וחכמת
השיעור
נוהגות המנהג
הזה ומועילות
במלאכות רבות,
שהן משמשות בחקות
התורה
ומצותיה,
ומצאנו הכתוב
במקומות הרבה
מצריך אליהן ...
ואין אדם יכול
לדקדק בחשבון עד
שלא יבוא בו
לידי הונאה,
אם לא ילמד
חכמת החשבון ...
ומי שאינו בקי
ורגיל בחכמת
השיעור אינו
מודד את
הארצות ולא
חולק אותה
באמת ובמשפט
בלא הונאה ...
ומכאן אתה למד
שהחכמות האלו
מצורך התורה
הן ... וראיתי
רוב חכמי
דורנו בארץ
צרפת אינן
בקיאים
במדידת
הארצות ולא
זריזים
בחלוקתן, אבל
הם מזלזלים
בדבר הזה
זלזול גדול
ומחלקין את
הקרקעות בין
היורשין
והשותפין לפי
אמידה וגוזמא
ובאין במעשה
הזה לידי עון
ואשמה ורובם
מזידים
וחוטאים וכל
אחד מהם חטאו
בטעותן כפי
שבוש
אומדנותן ...
שאין בעולם
הונאה הגדולה
מן ההונאה
הבאה על ידם ...
והקורא
ישים אל ליבו,
שחכמי צרפת
היו בקיאים בתורה
בקיאות גדולה,
ועדיין באו
לידי טעות כדברי
ראב"ח הנ"ל[17].
גם מידת
ה"חיצוניות"
שבחכמות
הקרויות
"חיצוניות"
מוטלת בספק.
רבי יהודה
הלוי[18]
אומר ב"ספר
הכוזרי":
ובאמת,
שורשי כל
החכמות
וכלליהן
הועתקו מאיתנו
אל הכשדים
בראשונה,
ואחרי כן אל
פרס ומדי, ואחרי
כן אל יוון,
ואחרי כן אל
רומא. אך מפאת
רוחק הזמן
וריבוי
המעתיקים לא
הוזכר בספרי
החכמות כי הועתקו
מעברית -
הוזכר רק כי
הועתקו
מיוונית ומרומית
...[19].
רעיונות
דומים נאמרים
גם על ידי
חכמים מאומות
העולם. תומסו
קמפנלה (Thomasso Campanella)[20],
במאמרו
"להגנת
גלילאו"[21]
(1616) אומר:
אמברוסיוס[22]
מעיד שפיתגורס
היה ממוצא
יהודי ...
פיתגורס ... הלך
בעקבות משה בתחיקה,
ולימד הכל
באמצעות
מספרים (... כמו
שעשו משה
ושלמה בבניית
המשכן ובית
המקדש ...).
השיטות של פיתגורס,
באותו אופן,
מסכימות עם מעשיהם
והתנהגותם של
היהודים ...
בספרי המכבים
נאמר
שהספרטנים הם
מגזע אברהם ...
בהתאם לעדותם
של לארטיוס,
אריסטו וגאלן,
פיתגורס
הודיע
לראשונה
לגויים את
עקרונותיו
המפליאים על תנועת
הארץ, על
מרכזיותה של
השמש, ועל
המערכות
שבשמיים ...
נראה
שעקרונות אלו
נלקחו ממשה,
שכן חכמה
גדולה כזאת -
לא יתכן
שתימצא מבלי
התגלות ... יתר
על כן, אריסטו
לעג למשה
העברי, וכן
לפיתגורס
ה"עברי" או
ה"מעוברת" ...
(מעניין
לציין
שבמקורות
שלנו יש
עדויות לכך שאריסטו,
בסוף ימיו,
היה לגר צדק[23]).
הרמב"ם
אומר[24]:
"וטעם כל אלו
החשבונות ...
היא חכמת
התקופות והגימטריות
שחברו בה חכמי
יוון ספרים
הרבה והם הנמצאים
עכשיו ביד
החכמים. אבל
הספרים שחברו חכמי
ישראל שהיו
בימי הנביאים
מבני יששכר לא
הגיעו אלינו",
ומרגיע:
"ומאחר שכל
אלו הדברים
בראיות
ברורות הם
שאין בהם
דופי, ואי אפשר
לאדם להרהר
אחריהם, אין
חוששין למחבר
בין שחברו
אותם נביאים
בין שחברו
אותם האומות,
שכל דבר
שנתגלה טעמו
ונודעה
אמיתתו
בראיות שאין
בהם דופי אנו
סומכין על זה
האיש שאמרו או
שלמדו על
הראיה
שנתגלתה
והטעם שנודע".
דברים אלו הם
בבחינת "חכמה
בגויים -
תאמין" (איכה רבה,
פרק ב').
במקומות
רבים בספרות
השו"ת מצאנו
פניות של גדולי
תורה
למתמטיקאים.
אילו היו
התלמוד והספרות
הרבנית
"מערכת
סגורה", למה
פנו למתמטיקאים
ולא לגדולי
תורה אחרים[25]?
והרי כמה
מהפניות: רבי
שמעון בן צמח
דוראן פונה
בענין הנ"ל
ל"מהנדס"
אנבלשום
אפרים גירונדי
לבירור אופני
חישוב נפחי
מקוואות
מיוחדים וזה
נימוקו:
"מיורק"א זה
שלחתי אל
אנבלשום אפרים
לפי שהיה בקי
בחכמת
התשבורת" (ראה
גם [16]). מהרי"ט[26]
פונה לרבי
יעקב בן יעיש,
שהיה בעל ידע
מתמטי [5, עמ' 144
הערה 2], בזו
הלשון: "ואין
לי שולחני
להרצות ספקותיי
זולתי האדון
אשר בגודל
חכמתך תאיר עיניי
בהלכה זו". רבי
יאיר בכרך[27]
פותח את סימן
קע"ד
בתשובותיו
"חוות יאיר"
במלים "תוך
כתבי לגדול
אחד אשר יצא
לו שם בידיעת חוכמה
זו הנ"ל[28]
אשר משכן
כבודו בק"ק
רחוקה ממני".
צא ולמד כמה
חשוב היה לו
לפנות לאדם
הבקי
במתמטיקה, עד
כי יפנה לקהילה
רחוקה ממנו.
יש
לציין כי בכל
המקורות
שהזכרנו
משתמשים העונים
במיטב הכלים
המתמטיים
שהיו בידיהם
באותו זמן.
נדגים ממספר
מקומות:
· אנבלשום
אפרים
גירונדי,
בתשובתו
לרשב"ץ, מסתמך
על משפט של
ארכימדס
המקשר בין נפח
גליל לנפח
כדור[29].
· רבי
יעקב בן יעיש,
בתשובתו
למהרי"ט,
מסתמך על משפט
פיתאגורס וכן
על משפטים של
פתולומיאוס (מספרו
The Almagest)
בנוגע לאורכי
מיתרים שונים
[5].
· רבי
יאיר בכרך
מזכיר יחס
שחישב
ארכימדס בין שטח
העיגול לשטח
הריבוע החוסם
אותו[30].
· הרב
סתהון מסתמך
בחישוביו על
משפט
פיתאגורס, וכן
על שיטת
האינטרפולציה
הלינארית
שהזכרנו קודם.
ויותר
ממה שהבאנו
כאן נמצא
לפנינו, וחלק
מהדברים
מצויים
במאמרינו
המפורטים
בסוף מאמר זה. יקראם
נא הקורא שם.
סיכום
ומסקנות
במהלך
המחקר הלכה
ונתרקמה לנגד
עינינו מסכת
ידיעות
ומתודות
חשיבה אוניברסליות,
עשירות
ורבגוניות,
ששימשו את
חכמינו הקדמונים.
עובדות אלה
מצטרפות
לעובדות אחרות
שמקורותינו
מלאים מהן,
המוכיחות כי
חכמינו לא
פעלו בתוך חלל
ריק, והמודל
של "מגדל
האור" הוא
שהניעם. מבין
הנוסחאות
והפורמליזם,
מצטיירת חברה
המהווה חלק
אורגני בחברה
הכללית, שמצד אחד
ידעה לשמור
בקפדנות על
ייחודה,
ומאידך ידעה
לברר את
ניצוצות
ה"חכמה
שבגויים"
ולספחם, ואף
לתרום משלה
לעיצוב תורת
החשיבה
האוניברסלית[31].
יש
להיזהר,
כמובן, מטשטוש
מוחלט של
הגבולות שבין
החלק
היהודי-ייחודי
בהיסק ההלכתי,
לבין החלק
האוניברסלי.
ההיסק
האוניברסלי אינו
יכול להפיק
אמיתות
הלכתיות יש
מאין. לשם כך
דרוש לו בסיס
הנתונים הרחב
שהוא מנת חלקה
של התרבות
היהודית,
ולעיתים אף
כללי היסק שהם
ייחודיים לה.
על כל פנים,
בחלקים
המתמטיים יש
לחלק
האוניברסלי
מקום רב
להתגדר בו.
רשימת
מאמרים
מרוכזת
א. של
כותבי מאמר זה
(לפי סדר לוגי)
עברית:
[1]
כל שיש
בהיקפו,
הגיון חוברת
ג', אלומה,
ירושלים: תשרי
תשנ"ו, 103 - 131.
[2]
סוכה עגולה,
מגל חוברת י',
המכון הגבוה
לתורה שע"י
אוניברסיטת
בר-אילן,
רמת-גן: תשנ"ד, 117 -
134.
[3]
סוכה עגולה (ב),
מגל חוברת י"א,
תשנ"ה, 127 - 134.
[4]
כוורת, המעין
ל"ה חוברת ג',
מוסד יצחק
ברייער של
פועלי אגודת
ישראל,
ירושלים: ניסן
תשנ"ה, 57 - 69.
[5]
עמוד שהוא
מוטל לאויר
(בהנחיית הרב
שמעון וייזר),
מגל חוברת י"א,
135 - 155.
[6]
חלון עגול,
בכתב יד.
[7]
על היחס שבין
היקף עיגול
לקוטרו, סיני,
כרך קי"ז, מוסד
הרב קוק,
ירושלים:
כסלו-טבת
תשנ"ו,
קפ"ו-קצ"א.
[8]
שיטת הרבנים
סתהון לחישוב
שרשים (עם
יאיר הלוי), מקרומטיקה,
תשנ"ח, 29 - 34.
[9]
לענין p
אצל סוכה, דף שבועי
מלימודי יסוד,
גליון 152,
אוניברסיטת בר-אילן,
רמת-גן: סוכות
תשנ"ז, 4 - 6.
אנגלית:
[10] On the Rabbinical Approximation of p, Historia Mathematica 25 (1998),
Academic Press, New-York, 75 - 84.
[11] The Proof of Rabbi Abraham Bar Hiya
Hanasi, in preparation.
ב. אחרים
עברית:
[12]
שמעון בולג, p
בספרות
התלמודית
והפרשנית, הגיון
חוברת ג', 92 - 102.
[13]
מיכאל בלייכר,
תירוץ על
קושיית החוות
יאיר בעניין
מדידת שטח
העיגול, קובץ
חידושי תורה
ופרפראות
לחכמה, בית
הספר הגבוה
לטכנולוגיה,
ירושלים:
תשמ"ד, 79 - 87.
[14]
מאיר ברכפלד, על
ניסוח פורמלי
ותלמוד תורה,
הגיון חוברת
ג', 7 - 8.
[15]
יחיאל מיכל
הכהן גוטמן, חיבור
המשיחה
והתשבורת,
הוצאת מקיצי
נרדמים,
ברלין: 1913.
[16]
יקותיאל
גינצבורג, אנבלשֵם
אפרים
גירונדי,
מתוך: יקותיאל
גינצבורג -
כתבים נבחרים,
הוצאת ספרים
מ. ניומן. תל
אביב/ירושלים:
תשכ"א, 151 - 168.
[17]
---, יעקב משה
מאירסון,
מתוך: יקותיאל
גינצבורג - כתבים
נבחרים, עמ' 194 - 228.
[18]
אסא כשר, למאמר
שלש בעיות
הנדסיות,
סיני, מוסד
הרב קוק,
ירושלים:
תשכ"ג, עמ' צ"ב -
צ"ד.
[19]
מתתיהו הכהן
מונק, שלש
בעיות
הנדסיות
בתנ"ך
ובתלמוד,
מוסד הרב קוק,
ירושלים: תמוז
תשכ"ב, 218 - 227.
[20]
---, דרכיה של
ההלכה בפתרון
בעיות
גאומטריות
מיוחדות,
הדרום חוברת
כ"ז, הסתדרות
הרבנים
דאמריקה, ניו-יורק:
ניסן תשכ"ח, 115 - 133.
שפות
אחרות:
[21]
William Moses Feldman, Rabbinical Mathematics and Astronomy, Hermon
Press, New-York: 1931.
[22] Grant Mccolley, The Defense of
Galileo, Arno Press, New-York: 1975. In: Smith College Studies in History,
Vol. 22, nos. 3 - 4.
[23] Benedict Zuckermann, Das
Mathematische im Talmud, Hepner, Breslau: 1878.