Theoretical exercise 1:

Consider the method

for solving the equation 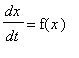, where are constants. Find the order of this method for all values of with

Practical exercise 1:

Suppose the scalar function satisifes the equation 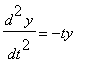with initial conditions y=1 and 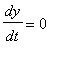when Write scilab or matlab functions to find y(1) and y(2) using any of the methods Euler, backward Euler, Heun, modified Euler, trapezoid, Runge-Kutta, with a user-determined number of (equal) steps. By comparing the errors for two different choices of the number of steps for each method, confirm that the orders of these methods are 1,1,2,2,2,4 respectively.

Start of solution:

1) We rewrite the equation as an autonomous first order system 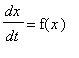where x is a dimension 3 vector and . We wish to find and when the initial condition is .

2) Here is code for scilab functions "f" and "feuler" that solve the problem using the Euler method.

//////////////////////

function y=f(x)

y(1)=1.0;
y(2)=x(3);
y(3)=-x(1)*x(2);

endfunction

//////////////////////

function a=feuler(n)

h=1.0/n;
x=[0.0;1.0;0.0];
for i=1:n 
  x=x+h*f(x);
end
a(1)=x(2)
for i=1:n 
  x=x+h*f(x);
end
a(2)=x(2);

endfunction

//////////////////////

Below we show results obtained from feuler(100000), feuler(40) and feuler(80). Treating the result of feuler(100000) as the exact result, we see the errors using 40 steps are roughly 0.0110 and 0.0141 , while for 80 steps they are roughly 0.0055 and 0.0069 . We see that halving the stepsize halves the error, consistent with order 1.

-->feuler(100000)
 ans  =
 
!   0.8388167 !
! - 0.0149732 !
 
-->feuler(40)
 ans  =
 
!   0.8498130 !
! - 0.0008768 !
 
-->feuler(80)
 ans  =
 
!   0.8443342 !
! - 0.0081179 !

3) Here is code for scilab functions "f", "beuler" and "by" that solve the problem using the backward Euler method.

//////////////////////

function y=f(x)

y(1)=1.0;
y(2)=x(3);
y(3)=-x(1)*x(2);

endfunction

//////////////////////

function a=beuler(n)

h=1.0/n;
x=[0.0;1.0;0.0];
for i=1:n 
  x=by(x,h);
end
a(1)=x(2)
for i=1:n 
  x=by(x,h);
end
a(2)=x(2);

endfunction

//////////////////////

function a=by(x,h)

eps=0.00001;
cha=eps*eye(3,3)
M=zeros(3,3)

a=x+h*f(x)
con=1

while(con>0)

  for i=1:3
     M(:,i)=(f(a+cha(:,i))-f(a))/eps
  end

  ch = (eye(3,3)-h*M)\(x+h*f(a)-a)
  con = norm(ch,1)
  a = a+ch

end 

endfunction

//////////////////////

Below we show results obtained from beuler(40) and beuler(80). Treating the result of feuler(100000) as the exact result, we see the errors using 40 steps are roughly 0.0112 and 0.0126 , while for 80 steps they are roughly 0.0056 and 0.0061. We see again that halving the stepsize halves the error, consistent with order 1. We also observe the fact mentioned in class that the errors in Euler and backward Euler are roughly the same in magnitude, just with reversed signs.

-->beuler(40)
 ans  =
 
!   0.8276534 !
! - 0.0275736 !

-->beuler(80)    
 ans  =
 
!   0.8332509 !
! - 0.0214623 !