scrap.html

Order Conditions for Runge Kutta Methods

The general Runge Kutta method for integrating x'=f(x) is as follows. Given an approximation to , we find , an approximation to , by (1) finding , ,..., , which satisfy (here s is the number of "stages" of the method, the are constants and ), and (2) setting (the w_i are also constants). If the are zero when j is greater than i we say the method is explicit.

We say the method is of order p if, assuming is exact, the error in is of order 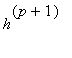. Order conditions (at least for relatively low orders) can be computed by simple Taylor expansions. There is a single order condition of orders 1 and 2, 2 of order 3 and 4 of order 4. These equations are given below:

> restart;

> e1:= sum(w[i],i=1..d)=1;

> e2:= sum(w[i]*sum(a[i,j],j=1..d),i=1..d)=1/2;

> e3:=sum(w[i]*sum(a[i,j],j=1..d)^2,i=1..d)=1/3;

> e4:= sum(w[i]*sum(sum(a[i,j]*a[j,k],k=1..d),j=1..d),i=1..d)=1/6;

> e5:=sum(w[i]*sum(a[i,j],j=1..d)^3,i=1..d)=1/4;

> e6:=sum(w[i]*sum(a[i,j],j=1..d)*sum(sum(a[i,j]*a[j,k],k=1..d),j=1..d),i=1..d)=1/8;

> e7:= sum(sum(w[i]*a[i,j]*(sum(a[j,k],k=1..d))^2,j=1..d),i=1..d)=1/12;

> e8:= sum(w[i]*sum(sum(sum(a[i,j]*a[j,k]*a[k,l],l=1..d),k=1..d),j=1..d),i=1..d)=1/24;

We are going to concerning oursleves with 4-stage explicit methods. In other words we set

> d:=4; a[1,1]:=0; a[1,2]:=0; a[1,3]:=0; a[1,4]:=0; a[2,2]:=0; a[2,3]:=0; a[2,4]:=0; a[3,3]:=0; a[3,4]:=0; a[4,4]:=0;

to get

> e1;

> e2;

> e3;

> e4;

> e5;

> e6;

> e7;

> e8;

There are 8 equations. We can get rid of w1,w2,w3,w4 which appear linearly:

> solve({e1,e2,e4,e8},{w[1],w[2],w[3],w[4]});

${w[2] = 1/24*(a[4,3]*a[3,2]^2+12*a[4,3]*a[3,2]^2*a[2,1]^2-a[3,2]*a[2,1]*a[4,1]-a[4,3]*a[3,2]*a[2,1]+2*a[4,3]*a[3,2]*a[3,1]-4*a[4,3]*a[3,2]*a[2,1]*a[3,1]+a[3,1]*a[4,2]*a[2,1]+a[4,3]*a[3,1]^2-4*a[4,3]*a[...$
${w[2] = 1/24*(a[4,3]*a[3,2]^2+12*a[4,3]*a[3,2]^2*a[2,1]^2-a[3,2]*a[2,1]*a[4,1]-a[4,3]*a[3,2]*a[2,1]+2*a[4,3]*a[3,2]*a[3,1]-4*a[4,3]*a[3,2]*a[2,1]*a[3,1]+a[3,1]*a[4,2]*a[2,1]+a[4,3]*a[3,1]^2-4*a[4,3]*a[...$
${w[2] = 1/24*(a[4,3]*a[3,2]^2+12*a[4,3]*a[3,2]^2*a[2,1]^2-a[3,2]*a[2,1]*a[4,1]-a[4,3]*a[3,2]*a[2,1]+2*a[4,3]*a[3,2]*a[3,1]-4*a[4,3]*a[3,2]*a[2,1]*a[3,1]+a[3,1]*a[4,2]*a[2,1]+a[4,3]*a[3,1]^2-4*a[4,3]*a[...$
${w[2] = 1/24*(a[4,3]*a[3,2]^2+12*a[4,3]*a[3,2]^2*a[2,1]^2-a[3,2]*a[2,1]*a[4,1]-a[4,3]*a[3,2]*a[2,1]+2*a[4,3]*a[3,2]*a[3,1]-4*a[4,3]*a[3,2]*a[2,1]*a[3,1]+a[3,1]*a[4,2]*a[2,1]+a[4,3]*a[3,1]^2-4*a[4,3]*a[...$
${w[2] = 1/24*(a[4,3]*a[3,2]^2+12*a[4,3]*a[3,2]^2*a[2,1]^2-a[3,2]*a[2,1]*a[4,1]-a[4,3]*a[3,2]*a[2,1]+2*a[4,3]*a[3,2]*a[3,1]-4*a[4,3]*a[3,2]*a[2,1]*a[3,1]+a[3,1]*a[4,2]*a[2,1]+a[4,3]*a[3,1]^2-4*a[4,3]*a[...$

> assign(%);

Note the need to assume , , all nonzero. Using the above values we reduce to 4 equations in the 6 a's. Simplifying a bit we need the following 4 quantities to vanish: