> p:=n->sqrt(n+1)-sqrt(n);

> evalf(p(100));

> evalf(p(1000));

> evalf(p(10000));

> evalf(p(100000));

seems p(n) -> 0

>

Many ways to do the next one. Let's try to find the value for n=1000

> n:=1000; s:=0; for i from 1 to n do s:=evalf(s+1/i) od: evalf(s-ln(n));

> n:=10000; s:=0; for i from 1 to n do s:=evalf(s+1/i) od: evalf(s-ln(n));

> n:=100000; s:=0; for i from 1 to n do s:=evalf(s+1/i) od: evalf(s-ln(n));

Seems to be converging to 0.5772.....

Another way (using "sum", which we didn't learn)

> p:=n->sum(1/z,z=1..n)-ln(n);

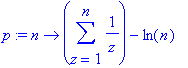
> evalf(p(1000));

> limit(p(N),N=infinity);

This is a constant known as "catalan's constant", gamma.

> evalf(gamma);

>

>

Next one.....

> n:=1000; s:=0; for i from 1 to n do s:=evalf(s+1/(n+i)) od: s;

> n:=10000; s:=0; for i from 1 to n do s:=evalf(s+1/(n+i)) od: s;

> n:=100000; s:=0; for i from 1 to n do s:=evalf(s+1/(n+i)) od: s;

Again seems to be converging

> p:=n->sum(1/(z+n),z=1..n);

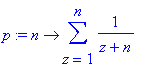
> evalf(p(10000));

> limit(p(N),N=infinity);

> evalf(ln(2));

>

> q:=n->n!*exp(n)/n^(n+1/2);

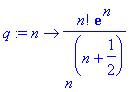
> evalf(q(10));

> evalf(q(100));

> evalf(q(1000));

also seems to be converging....

> limit(q(N),N=infinity);

> evalf(sqrt(2*Pi));

>