Question 1

> f:=x->x^3*exp(3*x)*cos(2*x);

> a1:=(D@@3)(f)(1);

> a2:=evalf(a1);

Question 2

> restart;

> f:=x->x^3*exp(3*x)*cos(2*x);

> a1:=int(f(x),x=0..1);

> a2:=evalf(a1);

Question 3

> restart;

> g(x):=exp(a*x)*cos(b*x);

> a1:=taylor(g(x),x=0,8);

> a2:=op(15,a1);

Question 4

> a3:=subs(a=cos(Pi/14),b=sin(Pi/14),a2);

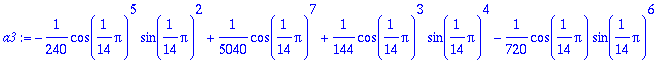
> combine(a3);

Question 5

> restart;

> f:=(exp(x)-exp(sin(x)))/x^3;

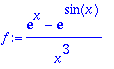
> limit(f,x=0);

Question 6

> h:=x->2-cos(x)+sin(x)-exp(x);

> Digits:=10; h(10.0^(-10));

> Digits:=20; h(10.0^(-10));

> Digits:=30; h(10.0^(-10));

> Digits:=40; h(10.0^(-10));

> Digits:=50; h(10.0^(-10));

> Digits:=60; h(10.0^(-10));

Question 7

> restart;

> fsolve(x^5-x-1/2=0);

Question 8

> restart;

> with(linalg):

Warning, the protected names norm and trace have been redefined and unprotected

> A:=matrix(4,4,[2.0,0,-1,1,0,2,0,1,0,-2,2,-2,2,-1,0,1]);

> ev:=eigenvects(A);

> ev[4][1];ev[4][3][1];

Question 9

> restart; with(linalg):

Warning, the protected names norm and trace have been redefined and unprotected

> A:=matrix(3,3,[a,1,1,1,1,1,1,1,1]);

> ev:=eigenvals(A);

> expand(ev[2]*ev[3]);

Question 10

> restart; with(linalg):

Warning, the protected names norm and trace have been redefined and unprotected

> v:=vector([sqrt(t)*cos(t),sqrt(t)*sin(t),t]);

> w:=map(p->diff(p,t),v);

> am:=dotprod(w,w,orthogonal);

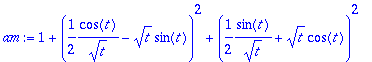
> an:=factor(simplify(am));

> sqrt(an);

=====================================================================

Question 1

> restart;

> f1:=x->sin(x) ; f2:=x->c*x*exp(-x);

> e1:= f1(a)=f2(a); e2:= D(f1)(a)=D(f2)(a);

> subs(c=solve(e1,c),e2);

> plot({cot(a),1/a-1},a=0..2*Pi,-4..4,discont=true);

> plot({cot(a),1/a-1},a=0..0.4,-4..40,discont=true);

> sol1:=fsolve({e1,e2},{a,c},a=1..3);

> sol2:=fsolve({e1,e2},{a,c},a=4..6);

> f:=piecewise(x<a,f1(x),f2(x));

> plot(subs(sol1,f),x=-10..20);

> plot(subs(sol2,f),x=-10..20);

Question 2

> restart;

> with(linalg):

Warning, the protected names norm and trace have been redefined and unprotected

> B:=matrix(3,3,[1,2,-2*s,6+s,3,1,1,-1,2]);

> p1:=charpoly(B,lambda);

> p2:=diff(p1,lambda);

B has two eqaul eigenvalues when if lambda=0 or 4. What does this mean for s?

> s1:=solve( subs(lambda=0,p1), s);

> s2:=solve( subs(lambda=4,p1), s);

> eigenvects( map( p->subs(s=s1[1],p) , B) );

> eigenvects( map( p->subs(s=s1[2],p) , B) );

> eigenvects( map( p->subs(s=s2[1],p) , B) );

> eigenvects( map( p->subs(s=s2[2],p) , B) );

The geometric multiplicity is always 1, even for the eigenvalue with algebraic multiplicity 2.

>

Question 3

> restart;

> Digits:=1005;

> p:=evalf(sin(1));

> for i from 1 to 1000 do p:=p*10: d[i]:=floor(p): p:=p-d[i]: od:

>

> for n from 0 to 9 do

> q[n]:=0:

> for j from 1 to 1000 do if(d[j]=n) then q[n]:=q[n]+1 fi: od:

> print(q[n]); od:

Question 4

> restart;

> with(plots):

Warning, the name changecoords has been redefined

> implicitplot(x^4+y^4=1,x=-1.5..1.5,y=-1.5..1.5);

> implicitplot(x^2+y^2=4/3,x=-1.5..1.5,y=-1.5..1.5);

> implicitplot({x^2+y^2=4/3,x^4+y^4=1},x=-1.5..1.5,y=-1.5..1.5);

> sol1:=fsolve({x^2+y^2=4/3,x^4+y^4=1},{x,y},x=-0.8..1,y=0.5..0.8);

> sol2:=fsolve({x^2+y^2=4/3,x^4+y^4=1},{x,y},y=-0.8..1,x=0.5..0.8);

I am not expecting the students to do the next bit......

If we work in polar coordinates r,theta we have r^2=4/3 and r^4 (sin^4 theta + cos^4 theta) = 1. So r = sqrt(4/3) and

sin^4 theta + cos^4 theta = 9/16. so (1-cos^2 theta)^2 + cos^4 theta = 9/16. Let's find cos theta:

> ct:=solve((1-c^2)^2+c^4=9/16 , c);

For each value of cos theta there are two values of sin theta. So we get 8 points. For example

> c:=1/4*sqrt(8+2*sqrt(2)): pt:=( sqrt(4/3)*c, sqrt(4/3)*sqrt(1-c^2));

> evalf(pt);

> I1:=int((1-x^4)^(1/4)-(4/3-x^2)^(1/2), x=pt[2]..pt[1]);

> evalf(I1);

==================================================================================================

>