Simplification

=========

Maple does some simplification automatically:

> restart;

> 1+2;

3

> x+x+x;

3*x

> x/x;

1

The last example is possibly dangerous: but if Maple did not do things like this it would be very hard

to work with. Many other things Maple does _not_ do automatically:

> x/y-2/y;

x/y-2/y

> cos(x)^2+sin(x)^2;

cos(x)^2+sin(x)^2

> sqrt(a^2);

sqrt(a^2)

"simplify": general purpose command, somehwat unpredictable

> simplify( x/y-2/y );

(x-2)/y

> simplify( cos(x)^2+sin(x)^2 );

1

> simplify( sqrt(a^2) );

csgn(a)*a

( csgn is the "complex sign function")

simplify is unpredictable:

> a:=(x+y+z)^2-(x+y)^2;

a := (x+y+z)^2-(x+y)^2

> b:=(x+y+z)^2;

b := (x+y+z)^2

> simplify(a);

2*x*z+2*y*z+z^2

> simplify(b);

(x+y+z)^2

Simplify has many types of rules it uses for simplifying expressions wiith sin and cos, ln and exp etc.

You can choose to only use some of these if you want, see ?simplify. Another option for simplify is

to let it make assumptions

> exp( ln(c) );

>

c

> ln( exp(c) );

ln(exp(c))

> simplify( ln( exp(c) ) );

ln(exp(c))

> simplify( ln( exp(c) ) , symbolic);

c

> simplify( sqrt(c^2) );

csgn(c)*c

> simplify( sqrt(c^2) , symbolic);

c

"expand": opens up brackets etc

> restart; b:=(x+y+z)^2;

b := (x+y+z)^2

> simplify(b);

(x+y+z)^2

> expand(b);

x^2+2*x*y+2*x*z+y^2+2*y*z+z^2

> c:=cos(x+y);

c := cos(x+y)

> simplify(c);

cos(x+y)

> expand(c);

cos(x)*cos(y)-sin(x)*sin(y)

> with(student):

> I1:=Int( x-x^2, x=alpha..beta);

I1 := Int(x-x^2,x = alpha .. beta)

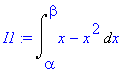
> I2:=expand(I1);

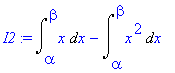
I2 := Int(x,x = alpha .. beta)-Int(x^2,x = alpha .....

"combine" does opposite of expand

> d:=expand(c);

d := cos(x)*cos(y)-sin(x)*sin(y)

> simplify(d);

cos(x)*cos(y)-sin(x)*sin(y)

> combine(d);

cos(x+y)

> e:=sin(7*x);

e := sin(7*x)

> f:=expand(e);

f := 64*sin(x)*cos(x)^6-80*sin(x)*cos(x)^4+24*sin(x...

> simplify(f);

64*sin(x)*cos(x)^6-80*sin(x)*cos(x)^4+24*sin(x)*cos...

> combine(f);

sin(7*x)

> I2;

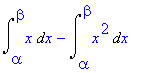
Int(x,x = alpha .. beta)-Int(x^2,x = alpha .. beta)...

> simplify(I2);

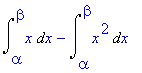
Int(x,x = alpha .. beta)-Int(x^2,x = alpha .. beta)...

> combine(I2);

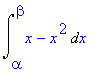
Int(x-x^2,x = alpha .. beta)

You sometimes need to tell combine to use a special set of rules:

> g:= w^x*(w^y+w^z);

g := w^x*(w^y+w^z)

> simplify(g);

w^(x+y)+w^(x+z)

> h:=expand(g);

h := w^x*w^y+w^x*w^z

> combine(h);

w^x*w^y+w^x*w^z

> combine(h,power);

w^(x+y)+w^(x+z)

Sometimes it is necessary to use 'assume' to get the result you want

> j:=ln(x)+2*ln(y);

j := ln(x)+2*ln(y)

> simplify(j);

ln(x)+2*ln(y)

> combine(j);

ln(x)+2*ln(y)

> combine(j,ln);

ln(x)+2*ln(y)

> assume(x>0,y>0);

> combine(j);

ln(x*y^2)

> restart;

Factor

> a:=(x+y-z-w)*(x-y+z-w)*(x-y-z+w)*(-x-y+z+w);

a := (x+y-z-w)*(x-y+z-w)*(x-y-z+w)*(-x-y+z+w)

> b:=expand(a);

b := -2*z^3*x-2*z^2*w^2-2*w^3*y-2*x*w*y^2+4*x*w^2*y...
b := -2*z^3*x-2*z^2*w^2-2*w^3*y-2*x*w*y^2+4*x*w^2*y...

> combine(b);

-2*z^3*x-2*z^2*w^2-2*w^3*y-2*x*w*y^2+4*x*w^2*y+2*x*...
-2*z^3*x-2*z^2*w^2-2*w^3*y-2*x*w*y^2+4*x*w^2*y+2*x*...

> factor(b);

-(x-y-z+w)*(x-y+z-w)*(x+y-z-w)^2

Collect

> collect(b,x);

-x^4+(2*z+2*w)*x^3+(-2*y*w-4*z*w-2*y*z+2*y^2)*x^2+(...
-x^4+(2*z+2*w)*x^3+(-2*y*w-4*z*w-2*y*z+2*y^2)*x^2+(...

> collect(b,[x,y]);

-x^4+(2*z+2*w)*x^3+(2*y^2+(-2*w-2*z)*y-4*z*w)*x^2+(...
-x^4+(2*z+2*w)*x^3+(2*y^2+(-2*w-2*z)*y-4*z*w)*x^2+(...

> collect(b,[x,y],distributed);

w^4-2*z^2*w^2+z^4+(-2*w-2*z)*y^2*x+(2*z+2*w)*x^3+(2...
w^4-2*z^2*w^2+z^4+(-2*w-2*z)*y^2*x+(2*z+2*w)*x^3+(2...

Finding values of expressions: eval and subs

> restart;

> a:=x^3;

a := x^3

> subs(x=2,a);

8

> eval(a,x=2);

8

> b:=diff(y(x),x,x)+y(x);

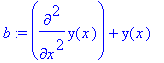
b := diff(y(x),`$`(x,2))+y(x)

> eval(b,y(x)=sin(x));

0

> b1:=subs(y(x)=sin(x),b);

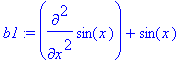
b1 := diff(sin(x),`$`(x,2))+sin(x)

> simplify(b1);

0

> c:=cos(x)/sin(x);

c := cos(x)/sin(x)

> eval(c,x=0); 

Error, division by zero

> subs(x=0,c);

cos(0)/sin(0)

> d:=x+y*z;

d := x+y*z

> subs([x=t,y=3],d);

t+3*z

> subs(x=t,y=x,d);

t+x*z

> subs(y=x,x=t,d);

t+t*z

> eval(d,[x=t,y=3]);

t+3*z

> eval(eval(d,x=t),y=x);

t+x*z

> eval(eval(d,y=x),x=t);

t+t*z