Integration

>

Simple indefinite integrals

> I1:=int( x^3*sin(2*x) , x ) ;

Simple definite integrals

> I2:=int( x^2*ln(x) , x=2..3 );

> I3:=int( ln(x)/x^2 , x=1..infinity);

Many special functions appear when doing integrals

> I4:=int ( ln(x)/(1+x) , x );

> I5:=int ( sqrt(1+x^3) , x=0..1 );

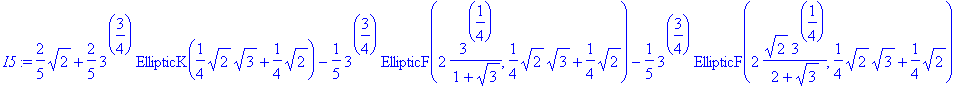
> evalf(I5);

Some integrals can simply not be done

> I6:=int( ln(1+x)*exp(-x^2) , x );

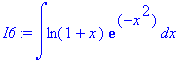
> I7:=int( sin(1+x^2)/(1+exp(x)) , x=0..1 );

>

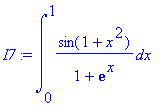
Maple is very good at integrals, but not good at writing the answer in the most sensible form.

Look at I8 below....the answer is real, but Maple uses I !!

Look at I9 below...the answer is equal to Pi*exp(-1) !!

> I8:=int( cos(x)/(1+x^2), x );

> I9:=int( cos(x)/(1+x^2), x=-infinity..infinity );

>

The student package

> with(student);

Int is an "inert" form of int:

> I10:=Int( x^3*sin(x), x);

intparts takes two arguments: the first is an unevaluated integral, the second is the factor to differentiate

> I11:=intparts( I10, x^3 );

> I12:=intparts( I11, x^2 );

> I13:=intparts( I12, x );

> I14:=intparts( I13, 1 );

changevar takes three arguments: the first is an equation defining x in terms of u, the second is an unevaluated integral, the third is the name of the new variable

> I15:=Int( x*sin(x^2), x);

> I16:=changevar( x^2=u, I15, u );

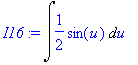
> I17:=Int( arcsin(x), x );

Sometimes Maple does not do what you want.....

> I18:=changevar( x=sin(u), I17, u);

> I19:=Int(u*cos(u),u);

To find the value of an unevaluated integral use "value"

> value(I19);

Partial fractions:

> a1:=(1+x^3)/(2+x+2*x^2+x^3);

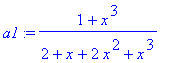
> a2:=convert(a1,parfrac,x);

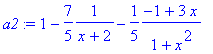
> a3:=1/(1+x^4);

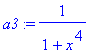
> a4:=convert(a3,parfrac,x);

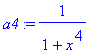
> a5:=convert(a3,parfrac,x,sqrt(2));

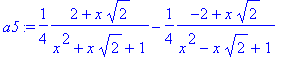
> a6:=convert(a3,parfrac,x,{sqrt(2),I});

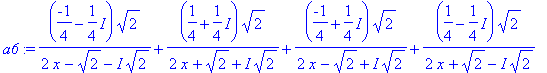
> a7:=convert(a3,parfrac,x,real);

>

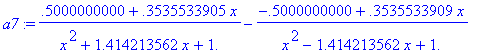
> int(a3,x);

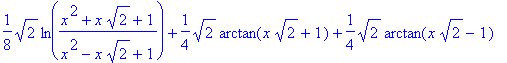
> int(a5,x);