10_recursion

כאשר פונקציה נקראת היא לוקחת מהזכרון מקום פנוי ומקצה אותו עבור הארגומנטים שלה ועבור משתנים פנימיים אחרים שלה.
שמות משתנים אלה אינם מוכרים מחוץ לפונקציה הנקראת. יתכן כמובן שבפונקציה הקוראת יש משתנים או פרמטרים בעלי שם זהה לאלה שבפונקציה הנקראת. דבר זה לא יפריע כלל לפעולת הפונקציה הנקראת.
כמובן שהפונקציה הנקראת יכולה גם היא לקרוא לפונקציה. ואפשר שתהיה גם שרשרת קריאות ארוכה יותר אך אסור שתהיה שרשרת קריאות אינסופית.
בכל קריאה לפונקציה יילקח מהזכרון. מקום עבור המשתנים והפרמטרים של הפונקציה הנקראת. עם סיום פעולת הפונקציה הנקראת ישוחרר מקום זה.
גם קריאה לפונקציה שאין לה פרמטרים ושגם אינה מכילה משתנים פנימיים צורכת זכרון. כי כל פונקציה יכולה להיקרא ממקומות שונים בתכנית ולכן צריך לדעת לאן לחזור אחרי שהביצוע שלה נגמר. לוקחים לכן מקום מהזכרון לשם שמירת כתובת החזרה לאחר הסיום.
נזכור גם שהופעת כותרת של פונקציה – אף ללא גוף הפונקציה - גורמת להכרת פונקציה זו החל ממקום ההגדרה ועד סוף הבלוק הפנימי ביותר המכיל אותה. טוח הכרה זה כולל כמובן גם את גוף הפונקציה, כלומר הגוף של פונקציה יכול להכיל קריאה לכל פונקציה שהכותרת שלה מוכרת במקום הקריאה. ה"כל" כולל גם את הפונקציה עצמה. כלומר מבחינה תחבירית הפונקציה הבאה תקינה : void a() {a();}

חזרה להתחלה

מהי פונקציה רקורסיבית

· פונקציה רקורסיבית היא פונקציה הקוראת לעצמה.

לולאה "אינסופית" ברקורסיה

אזהרה !!!! לפני שתנסה את התכנית הבאה אנא לטובך בצע SAVE בכל התכניות שבמחשב !!!

void a() { a(); }

void main()

{

a();

}

תוכנית זו הורצה והמערכת ( חלונות 98 ) נפלה.

הסיבה: למרות שאין כאן פרמטרים ואין משתנים בכל זאת כל קריאה לוקחת זיכרון חדש ( מהמחסנית – STACK ) לצורך שמירת מקום הקריאה.

מספר הקריאות גדל ללא הגבלה, לכן יגיע מצב שבו כל הזיכרון ייתפס והתכנית לא תוכל להמשיך ולפעול. ( מצב ביש זה עלול לגרום במערכות שונות לתקלות שונות ).

תנאי עצירה לרקורסיה

void a(int n)

{

if ( n==0 ) // stopping condition

return;

a(n-1);

}

void main()

{

a(4);

}

במקרה זה ברור ש a לא רק שתעבור הידור אלא גם תרוץ ללא דופי.

יש לנו כאן בדיוק 5 קריאות ל a . כל קריאה חדשה נעשית עם n קטן יותר. לאחר 4 קריאות נגיע לקריאה החמישית שתהיה a(0). קריאה זו תהיה האחרונה.

· התנאי (n==0) שמופיע בתחילת הגוף של a הוא תנאי עצירה .פונקציה רקורסיבית תפעל בצורה תקינה רק אם יש בה תנאי עצירה.

· רצוי לכתוב את תנאי העצירה באופן מפורש וכפקודה ראשונה אחרת עלולים לשכוח אותו . הפונקציות a1, a2 שקולות לa אך ראוי שלא לכתוב כך.

void a1(int n) // BAD STILE of stopping ocndition.

{ if (n != 0)

a1(n-1);

else return;

}

void a2( int n) // BAD STILE of stopping ocndition.

{

if(n != 0)

a2(n-1);

}

· נוסיף ל a פקודת הדפסה ונקבל:

#include <iostraem.h>

void a3 ( int n)

{

if (n==0)

{ cout << n << endl;

return;

}

cout << n << " ";

a3(n-1);

}

void main()

{

a3(4);

}

-----------------------Output-----------------------

4 3 2 1 0

1. נראה עתה כי אם נקרא ל a3(n) נקבל הדפסה של סדרת המספרים מ n ועד 0 בסדר יורד.

2. אפשר לראות זאת באינדוקציה:

אם n=0 אזי ברור ש A3(0) תדפיס רק את 0 .

נניח ש a3(n-1) מדפיסה את: n-1 n-2 n-3 . . . 2 1 0

בעת קריאת n3(n) קודם כל יודפס n ואחר כך תהיה קריאה ל a3(n-1) שתדפיס , לפי הנחת האינדוקציה, את שאר הסדרה.

רקורסית זנב tail recursion

· רקורסית זנב (tail recursion) היא רקורסיה שבה הקריאה העצמית נעשית רק כפקודה האחרונה שבפונקציה.

· קל להפוך רקורסית זנב ללואה.

· מהדירים רבים ימירו רקורסית זנב ללואה.

· אדם שהרגיל עצמו לחשיבה רקורסיבית יפתור במהירות רבה יותר בעיות רבות.

· מחשב יבצע בדרך כלל לולאה במהירות רבה יותר.

· לכן כדאי לאדם לחשוב רקורסיבית אך לכתוב אם אפשר רקורסית זנב. המהדיר כבר ידאג להמרה ללולאה.

· במקרה שלנו a3 תהיה :

void a3(int n)

{

while (n >= 0)

cout << n-- << " ";

}

נשנה מעט את a3 ( הרקורסיבית ) נעביר את פקודת ההדפסה מתחילת הפונקציה לסופה ונקבל את a4:

#include <iostraem.h>

void a4(int n)

{

if (n == 0)

return;

a4(n-1);

cout << n << " ";

}

void main()

{ a4(4);

}

-----------------------Output-----------------------

1 2 3 4

לכאורה ההבדל היחיד הוא ש a4 איננה כתובה ברקורסית זנב.

אך מבט רגיש יותר יראה לנו שהשוני בכתיבה גרם שוני בביצוע. אנו מדפיסים את n אחרי שהודפסה כבר הסדרה הנוצרת על ידי a4(n-1) .

4 יודפס אחרי שהודפסה הסדרה המתאימה ל a4(3) , 3 יודפס אחרי הסדרה שהודפסה על ידי a4(2) וכו'.

לא קבלנו 0 1 2 3 4 כפי שאפשר היה אולי לצפות בטעות. 0 לא הודפס! בקריאה a4(0) אין מבצעים דבר אלא חוזרים מיד! .

· מסקנה: יש תמיד להקדיש תשומת לב מיוחדת למקרה האלמנטרי – המצב שבו מתמלא תנאי העצירה. אנו עלולים להתעלם ממנו ולקבל תוצאות לא צפויות.

· אם נשאיר את פקודת ההדפסה הן בהתחלה והן בסוף נקבל:

4 3 2 1 0 1 2 3 4

ועבור n כל שהוא נקבל מקריאת A ( n ) את ההדפסה :

n n-1 n-2 … 3 2 1 0 1 2 3 … n-1 n

· אנו יכולים להדפיס מספרים לסרוגין על ידי התכנית:

#include<iostraem.h>

void a(int n)

{ cout << n << ' ';

if(n == 0)

return;

a(n-2); // n-2 instead n-1

cout << n << ' ';

}

void main ( )

{

a(4);

}

-----------------------Output-----------------------

4 2 0 2 4

· אך אם נכתוב ב main a(5) נקבל רקורסיה אין סופית והדפסה אין סופית שתתחיל ב :

5 3 1 -1 -3 -5 -7 ……….

· כמובן שלאחר שהרקורסיה תשתמש בכל הזיכרון שבמחסנית תהיה תקלה שתגרום לעצירה לא תקינה.

· הצרה נגרמה על ידי חוסר תשומת לב למצב העצירה. לעולם לא נגיע למצב שבו n = 0 . ( "מצב" : ו מכלול ערכי המשתנים בתכנית)

· חובה להבטיח שעבור כל ארגומנט אפשרי נגיע לבסוף למצב עצירה. נרשה לפונקציה לקרוא לעצמה אך ורק אם המצב יהיה פשוט יותר. כלומר או שהארגומנט (ארגומנטים) יהיו פשוטים יותר או שמשתנה חיצוני המוכר בפונקציה יהיה פשוט יותר.

· ה"פשטות" הזו פרושה הוא שעל ידי הפעלתה שוב ושוב נגיע לאחר מספר צעדים סופי למצב אלמנטרי – מצב עצירה.

· בדוגמא האחרונה המצב n = 3 אינו פשוט יותר מהמצב n=5 כי הוא לא מקרב אותנו למצב עצירה.

· נתקן את תנאי העצירה.

· במקום התנאי “ n == 0 “ שאינו עוצר נכתוב: " n <= 0 " .

· הפעם נקבל את הסדרה: 5 3 1 -1 1 3 5 .

( שים לב למופע של -1 !!! )

רצוי היה לתקן את תנאי העצירה גם בכל הדוגמאות הקודמות.

הנחנו כְּמובן מאליו שתמיד הארגומנט n אינו שלילי. הנחה כזו יכולה להיות מוצדקת בעת כתיבת התכנית. אך לאחר זמן התכנית יכולה לעבור שינויים. יכולים להשתמש בה גם עבור מקרים שלא חשבנו עליהם מראש. על כן יש תמיד לחשוב על מקרים בהם הקלט "לא תקין" ולטפל בהם. בדוגמאות דלעיל מספיק להחליף את תנאי העצירה “n == 0“ ב: " n <= 0 " .

באופן כללי אפשר לנהוג באחת הדרכים:

להחליף את תנאי העצירה בתנאי המתאים לכל מקרה . ( כגון : כתיבת התנאי n <= 0 )

· להוסיף בגוף הפונקציה בדיקה למקרים חריגים. בדיקה כזו צריכה להעשות לפני קריאה רקורסיבית מתוך הפונקציה.

לדוגמא: כגון החלפת: הפקודה a(n-2) בפקודות:

if(n % 2) return;

a(n-2)

פונקצית הכנה לפני הקריאה לפונקציה הרקורסיבית

#include <iostream.h>

void _a( int n) // אין בדיקות תקינות בפונקציה A

{

cout << n << ' ';

if ( n==0 ) return;

_a(n-2); // n-2 instead n-1

cout << n << ' ';

}

void a(int n) // _a ‘s correctness checking

{

if (n % 2 )

{ cout << "ERROR: a got " << n <<

"as argument ,while the input must be a non-negative even num.";

return;

}

_a(n) ;

}

void main()

{ a(10);

cout << endl;

a(11);

}

-----------------------Output-----------------------

10 8 6 4 2 0 2 4 6 8 10

ERROR: A got 11 as argument ,while the input must be a non-negative even num.

· הפונקציה a אנו בודקת תקינות רק בקריאה בודדת ולא בכל קריאה רקורסיבית.

סיכום ביניים והערות עקרוניות

· בהפעלת פונקציה רקורסיבית עלולה להתעורר בעיה של שרשרת קריאות אין סופית.

· לכן כדי להבטיח שפונקציה המפעילה את עצמה אמנם תעצור הכרחי שלפונקציה רקורסיבית תהינה שתי תכונות:

א. קיום מצבים בסיסיים (לפחות אחד) שבהם הפונקציה עוצרת.

ב. קריאה לפונקציה במצב פשוט יותר, או מספר קריאות במצבים פשוטים יותר, כאשר המצב אינו בסיסי.

הערות לאדם החושב: פונקציה רקורסיבית אינה מיצגת "הגדרה מעגלית". הגדרתה אינה כוללת את עצמה. אנו מגדירים את הפונקציה הפועלת על רשימת פרמטרים כלומר מגדירים זוג (מצב , פונקציה). הגדרה זו מתבססת על הגדרת הפונקציה לגבי מצב פשוט יותר כלומר מתבססת לא על עצמה אלא על זוג : (מצב , פונקציה) פשוט יותר. את תקינותה של ההגדרה הרקורסיבית אפשר להוכיח באינדוקציה על אורך סדרת המצבים המסתימת במצב פשוט.

במקרה שהפונקציה מכילה מספר קריאות לעצמה כמו בדוגמאות הminimax והזוג-פרד דלהלן מקבלים עץ קריאות במקום סדרת קריאות כבמקרה של קריאה בודדת. הקורא המתמצא במבנה עצים יוכל להעביר את מה שנכתב לגבי הסדרה גם לגבי העץ. הדרישה תהיה שעץ הקריאות יהיה בעל עומק סופי, והוכחת התקינות תהיה באינדוקציה על עומק העץ.

אי אפשר "לדרוש מהמחשב" שבכל מקרה שבו תכנית תכיל פונקציה רקוסיבית הוא יבדוק אם פונקציה זו תעצור עבור כל ערכי פרמטרים שתקבל. קיימת הוכחה ל,משפט העצירה" הטוען שאין אלגוריתם הקובע לכל תכנית אם היא תעצור. ( ה"אין" כולל את האלגוריתמים שנכתבו ואת אלה שאיש טרם חשב עליהם). המהדירים בודקים רק את התקינות התחבירית. לכן לצרכים מעשיים כגון פיקוח על הליך בתעשיה או בתקשורת, כדאי לעיתים לכתוב אלגוריתם רקורסיבי ( כגון אלגוריתם עם רקורסית זנב) אלגוריתם זה ירוץ לנצח – כלומר עד הפסקת החשמל הקרובה.

חזרה להתחלה

פתרון בעיות ברקורסיה

דוגמא קילוף הבצל

ספר בישול מכיל מתכון בשם "עלי בצל". ההוראות לקילוף הבצל הן:

אם אין עלים סיימת את הקילוף. אחרת הסר עלה מהבצל וקלף את הבצל שנשאר.

דוגמא למימוש המתכון:

class onion {

int _leafs; // number of leafs

public:

onion(int l) : _leafs(l) {}

void one_leaf_off() { if(_leafs > 0) _leafs--;}

int leafs() const { return _leafs; }

};

void kalef(onion x)

{

if(x.leafs() == 0)

return; // do nothing in case there is no onion anymore.

x.one_leaf_off();

kalef(x);

}

בצוע פונקציה זו הוא פשוט בתכלית.

אתה מקבל בצל. אם הבצל הזה הוא פיקטיבי (דהיינו לא קבלת כלום) אינך עושה דבר.

אחרת אתה מקלף קליפה אחת. ולגבי מה שנשאר אתה מפעיל את אותה פונקציה.

ברור שלגבי כל בצל התהליך יגמר כי מספר קליפותיו הולך וקטן ולבסוף נקבל בצל ריק ונעצור.

דוגמא מציאת MAX במערך

בעיה: נתון מערך A[n] של מספרים ממשיים. צריך למצוא את המספר המכסימלי במערך.

השיטה :

אם n=0 המערך הוא באורך 1 , יש בו מספר בודד , ומספר זה הוא המכסימום .
אם יש בו יותר ממספר אחד אזי:

i. הצב במשתנה a את המכסימום של האיברים A[0 … n-1 ] ( קְרִי - A[0] עד A[n-1] ):

ii. המכסימום הכללי הוא הגדול שבין המספרים: a A[n] , .

את המקרה n > 0 נוכל לנסח גם בלי שימוש במשתנה העזר a :

המכסימום הכללי הוא הגדול שבין שני המספרים A[n] והמכסימום של A[ 0 … n-1 ] .

הנוסחא הבאה מגדירה את השיטה כולה:

ברור שהנוסחא הנ"ל נכונה. למעלה מכך הנוסחא הזו לא רק מספרת על איזו תכונה נחמדה של המכסימום הכללי , היא גם מְחַשֶבֶת את המכסימום הכללי!. נוכיח שאמנם הנוסחא מחשבת את המכסימום עבור כל מערך.

הוכחה באינדוקציה:

המקרה n=0 , מקרה עצירה, הפונקציה פועלת כראוי.

המקרה n>0

נניח שהפונקציה פועלת כראוי לכל k<n .

תחשב את המכסימום של A[ 0 … n-1 ] ולכן השורה השניה כולה תחשב את הדרוש.

( הערה: הוכחת נכונות פונקציה רקורסיבית נעשית תמיד באינדוקציה).

התכנית הבאה היא תרגום של הנוסחא ל C++.

#include <iostream.h >

#include <stdlib.h> // max()

double maxarray(double a[] , int n)

{

if ( n == 0 ) return a[0];

return max (a[n] , maxarray(a, n-1)); }

void main()

{

const int n = 9;

double a[n];

for(int i=0; i<=n ; i++) cin >> a[i];

cout << maxarray(a, n);

}

דוגמא מציאת MINIMAX במערך

בעיה: נתון מערך של מספרים ממשיים. צריך למצוא את המספר המכסימלי במערך ואת המספר המינימלי.

השיטה : אם המערך הוא באורך 1 , יש בו מספר בודד , ומספר זה הוא גם מכסימום וגם מינימום.

אם יש בו יותר ממספר אחד. נחלק אותו לשני חלקים בעלי מספר איברים שוה ככל האפשר.

נמצא מינימום ומכסימום בכל חלק. המספר הגדול בין הגדולים יהיה המכסימום הכללי, והקטן בין הקטנים יהיה המינימום הכללי. הקורא מתבקש להוכיח לעצמו שאמנם בדרך זו נקבל את הדרוש.

דוגמא :

פרקנו את המערך לשני קטעים האחד בן 5 איברים והשני בן ששה.

זוג המינימקס של המחצית השמאלית הוא (3,71) וזה של הימנית הוא (11,77) האיבר הקטן שבין הקטנים הוא 3 הגדול שבין הגדולים הוא 77 ועל כן המינימכס הכללי הוא (3,77) .

קבענו בפשטות שהמינימכס של המחצית השמאלית הוא ( 3 , 71 ) . איך אפשר לדעת זאת? התשובה פשוטה בעזרת הפונקציה מינימכס! . אנו מחלקים את המחצית הראשונה לשנים מוצאים בכל מחצית מינימכס וכו'. התהליך הוא סופי כי בכל פעם המחציות קטנות יותר. ולבסוף נגיע למחצית שגודלה 1.

#include <iostream.h >

#include <stdlib.h> // 4 min , max

#include <math.h> // 4 floor

class pair {

public :

pair (double , double ):first(f), second(s) {}

void show ( ) { cout << first << ' ' << second << endl; }

double first , second ;

};

pair minimax (double a[] , int left , int right )

{

if ( left == right )

return pair (a[left], a[left]);

pair y = minimax(a, left, floor((left+right) / 2));

pair z = minimax(a, floor((left+right) / 2) + 1 , right);

return pair(min(y.first, z.first), max(y.second, z.second));

}

void main()

{ const int n = 11;

double A[n];

for ( int i = 0; i < n ; i++)

cin >> A[i];

minimax(A, 0, n-1).show();

}

חישוב n!

חשב את

פתרון: הנוסחא הבאה מגדירה את n! לכל מספר טבעי

לצרכים שונים נח להרחיב את ההגדרה של n! גם עבור ולהגדיר 0! = 1 .

נוסיף על כן מצב בסיסי נוסף: וההגדרה החדשה תהיה:

הגדרה זו שקולה להגדרה :

בשפת ++C

	long int factorial ( int k )
	{
	if ( k == 0 ) return 1;
	return k factorial( k-1) ;*
	}

זוג ופרד

נסתכל בפונקציה הבאה

עבור n נקבל את הסדרה הבאה . ( נתחיל ב n ואחרי כל מספר נכתוב את ה next שלו . נעצור אם נגיע ל 1.

עבור n=7 נקבל:

7 22 11 34 17 52 26 13 40 20 10 5 16 8 4 2 1

האם מובטחת הגעה למצב עצירה ?

משערים שכן , אך לא ידועה הוכחה לכך.

אם נסתכל על הבעיה בגישה רקורסיבית אזי ניצור את הסדרה המתאימה ל n באופן הבא:

נכתוב את n ואחריו את הסדרה המתאימה ל next(n) .

בכדי למעט בבדיקות לקביעת next(n) נכתוב פונקציה מיוחדת zug ל n זוגי , ופונקציה מיוחדת pered ל n פרד ( "פרט" בלשון בתי הספר).

המספר הבא אחרי מספר פרד , שונה מ1, הוא מספר זוג. אחרי זוג יכול לבוא או זוג או פרד.

נקבל כאן מקרה של שתי פונקציות שבכל אחת יש קריאה לשניה.

על כן הכרחי להכריז על כותרות לפני הגדרת הגוף.

#include <iostream.h>

#include <iomanip.h>

class sequence

{ public:

void printseq (int );

private:

void zug(int );

void pered ( int );

int num_in_row ; // מספר המספרים שיודפסו בכל שורה

int numwidth ; // רוחב השדה שבו יודפס כל מספר

char printed ; // כמה מספרים הודפסו עד כה בשורה הנוכחית

};

void sequence::printseq(int k)

{ num_in_row =8;

numwidth =7;

printed = 0;

if ( k % 2 ) pered (k);

else zug ( k );

}

void sequence::zug (int k)

{ cout << setw ( numwidth ) << k;

if (++printed == num_in_row)

{ printed =0; cout <<"\n"; }

k=k / 2;

if (k % 2) pered ( k ); else zug ( k ) ;

}

void sequence::pered(int k) // called only when k is even.

{ cout << setw ( numwidth ) << k ;

if (++printed == num_in_row)

{ printed =0; cout << '\n'; }

if (k != 1 ) zug ( k*3+1) ;

}

void main ( )

{ sequence s;

s.printseq ( 7 ) ;

}

---------------------------- output ---------------------

הפלט:

7	22	11	34	17	52	26	13
40	20	10	5	16	8	4	2
1

אם נרצה "קריאה רגילה לפונקציה" ( printseq ( 7 ) ; ) מתוך main נצטרך לותר על השימוש במחלקה, וממילא נותר על יתרונות תכונת הכימוס. נגדיר את שלוש הפונקציות: sequence, zug, pered כפונקציות גלובליות. כאן תיוצר בעיה: שפת ++C דורשת הגדרת מזהים לפני השימוש בהם ( הדבר מקל על תהליך ההדרה). כל אחת מהפונקציות zug, pered משתמשת בפונקציה האחרת. ולכן לכאורה כל אחת צריכה להכתב אחרי השניה!

ואולם כאשר קיימת קריאה לפונקציה המהדיר צריך לדעת לערוך את רשימת הארגומנטים כראוי. לשם כך הוא צריך לדעת את מספר הארגומנטים שיש לשלוח לפונקציה ואת האפיון של כל ארגומנט. הוא צריך גם לדעת את אפיון הערך המוחזר. לצורך הידור הקריאה והשימוש בערך המוחזר אין כל צורך בהכרת גוף הפונקציה.

נכתוב על כן תחילה את ההצהרות של שלוש הפונקציות ולאחר מכן את הפונקציות בשלמותן.

( אפשר היה להקפיד על סדר כתיבת הפונקציות ולהסתפק בהצהרה מראש של פונקציה אחת בלבד מביו הפונקציות zug, pered ).

נקבל את התכנית הבאה:

void printseq (int k);

void zug(int );

void pered(int stam_mishtane);

void printseq (int k)

{ printseq הגוף של }

void zug (int k)

{ zug הגוף של }

void pered(int k)

{ pered הגוף של }

void main()

{ printseq (23)

}

שים לב: לאחר שורת ההצהרה על פונקציה בא הסימן ; .

ברשימת הארגומנטים שבהצהרת פונקציה אפשר להשמיט את שם הארגומנט, או
לכתוב שם כל שהוא.

חזרה להתחלה

הרקורסיה במדעי המחשב

הרקורסיה משמשת במדעי המחשב לא רק לפתרון בעיות אלא גם להגדרת מושגים.

לדוגמא אם אנו רוצים להגדיר מה הוא ביטוי תקין נגדיר ראשית ביטויי יסוד, ובנוסף לכך נקבע שביטוי הנבנה מביטויים אחרים בעזרת פעולות חוקיות הוא ביטוי תקין אם הביטויים האחרים הם ביטויים תקינים .

אפשר להגדיר "ביטוי אריתמטי " כך: ביטוי אריתמטי יסודי הוא מספר או משתנה-מספר. וביטוי הוא ביטוי אריתמטי אם הוא נבנה מביטוי אריטמטי או משני ביטויים אריתמטיים בעזרת סוגריים וארבע פעולות החשבון: " / , * , - , + " .

אפשר להגדיר ביטויים המכילים פעולות נוספות כגון שורש, חזקה, פונקציות טריגונומטריות וכו' וכו'. הגדרות כאלו מאפשרות למהדיר לבדוק חוקיות של ביטויים המופיעים בתוכנית. הגדרת ביטויים על ידי סדרה אין סופית של ביטויים אינה נחשבת להגדרה תקינה. אנו דורשים שאם נפרק ביטוי לביטויים פשוטים יותר ונחזור ונפרק נגיע אחרי מספר סופי של פרוקים לביטויים יסודיים.

השוואת פתרון רקורסיבי לפתרון איטרטיבי

ניסוח פתרון רקורסיבי לבעיה הוא קל ופשוט מאשר ניסוח פתרון איטרטיבי. בעת חשיבה על פתרון איטרטיבי אנו חושבים על תהליך הכולל שלבים רבים בעוד שבחשיבה על תהליך רקורסיבי אנו חושבים על שלב בודד: העברת הבעיה למקרים פשוטים יותר. אנו חושבים בשיטת הפרד-ומשול. מפרידים את הבעיה למספר בעיות פשוטות - כמו במקרה של minimax או מעבירים את הבעיה לבעיה פשוטה יותר.

קצת פסיכולוגיה

קיימים אנשים שכאשר מראים להם תמונה תלת-מימדית הם מתרכזים בכל כוחם כדי לראות בדייקנות את הפרטים שבתמונה ולכן אינם רואים כלום. אלה שמסתכלים על התמונה בכללותה רואים את פרטי התמונה.

ברקורסיה ה"תמונה בכללותה" היא העברת הבעיה לבעיה דומה אך פשוטה יותר ( או מספר בעיות פשוטות יותר) . ה"פרטים" הם פתרון הבעיה הפשוטה יותר על ידי העברתה לבעיה פשוטה עוד יותר ,פתרון הבעיה הפשוטה עוד יותר על ידי העברתה לעוד יותר פשוטה וכו' וכו'.

בדוגמת הminimax ה"תמונה הכללית" היא פרוק קבוצת המספרים לשתי קבוצות פשוטות יותר. ה"פרטים" הם : טיפול בכל תת-קבוצה של מספרים וכו' וכו' .

קצת היסטוריה

לסיום הערה היסטורית: מקובל לראות ב QUICKSORT את הפתרון הרקורסיבי הראשון לבעיה. ואולם בספרו היד החזקה (נשים, אישות, יז ,ח) כותב הרמב"ם ( בעקבות הרי"ף) ניסוח רקורסיבי מושלם לפתרון בעיית חלוקת הרכוש של פושט רגל. ניסוחו הרקורסיבי בולט בקיצורו על

רקע האריכות של הניסוח האיטרטיבי שאותו כתב רבי יהודה בן ברזילי מברצלונה. בעל הבאור "מגדל עוז" על היד החזקה כותב שם שיר הלל

מחורז, לעדיפות הקיצור של הנוסח (הרקורסיבי) הנ"ל על פני אריכות הנוסח האיטרטיבי: " הרב הברצלוני ז"ל כתב בה דרך ארוכה מארץ מדה

ורחבה מני ים, אמנם, ר"מ ז"ל (הרמב"ם), לימד דרך קצרה מובחרת, מפי רבותיו מקובלת, ויפה עשה וכיון לבו, שחייב אדם לומר כלשון רבו".

מעתיקים ומדפיסים שלא הבחינו בהדר המיוחד של הפונקציה הרקורסיבית הנ"ל צרפו לסעיף ח' המקורי את שני סעיפי הדוגמאות הבאים אחריו. ( ראה חוברת "הגיון" כרך ב').

חזרה להתחלה

דוגמאות נוספות לרקורסיות

בעית מגדלי הנוי Hanoi

0

1

2

הבעיה:

כיצד להעביר n טבעות מעמוד 0 לעמוד 2 (בדוגמא n הוא 3), כאשר מותר להעביר בכל פעם טבעת אחת, אך אסור שטבעת גדולה תהיה מונחת על טבעת קטנה.
הבעיה הוצגה ע"י המתמטיקאי הצרפתי Edouard Lucas בשנת 1883.

השיטה הרקורסיבית לפתרון: נניח כי אנו יודעים כיצד לפתור בעיה קטנה יותר של העברת (n-1) טבעות. אז הפתרון לבעיה כולה ניתן באופן הבא:

1. מעבירים את כל הטבעות הקטנות פרט לגדולה מכולן לעמוד הנוסף (1).

2. מעבירים את הטבעת הגדולה לעמוד המתאים (2).

3. מעבירים את הטבעות הקטנות על גבי הגדולה.

נדגים כאשר n = 3:

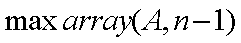
0

1

2

0

1

2

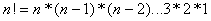
נדגים עוד רק את פתרון הבעיה הקטנה הראשונה (להעביר טבעות C B מעמוד 0 לעמוד 1 בעזרת עמוד 2) ולא את יתר שלבי פתרון הבעיה:

1. נעביר את כל הטבעות העליונות מעל B (הטבעת C בלבד) לעמוד הנוסף שהוא 2.

2. נעביר את הטבעת B לעמוד 1.

3. נעביר את כל הטבעות (הטבעת C) מעמוד 2 לעמוד 1.

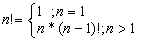
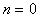
// ....... PILLAR.H ....................

typedef char Ring;

const int MaxRings = 20;

class Pillar {

public:

Pillar();

void PlaceRings(int sz);

void Show();

Ring Pop();

void Push(Ring r);

private:

int n; // number of rings.

Ring rings[MaxRings];

};

class Pillars {

public:

Pillars(int n);

void Show();

void MoveRing(int from, int to);

private:

int steps;

Pillar p[3];

};

//........ PILLAR.CPP ....................

#include <iostream.h>

#include "PILLAR.H"

Pillar::Pillar() : n(0) {}

void Pillar::PlaceRings(int sz)

{ for (int i = 0, n = sz; i < sz; i++) // also initializes n.

Push('A' + i); // assumes ascii representation.

}

void Pillar::Show()

{ for (int i = 0; i < MaxRings; i++)

cout << (i < n ? rings[i] : ' ');

}

Ring Pillar::Pop()

{ return rings[--n]; }

void Pillar::Push(Ring r)

{ rings[n++] = r; }

Pillars::Pillars(int n) : steps(0) // same as steps = 0

{ p[0].PlaceRings(n); } //init. pillar0, others by default construc.

void Pillars::Show()

{ cout << setw(3) << steps++;

for (int i = 0; i < 3; i++)

{ cout << " Pillar" << i << ": ";

p[i].Show();

}

cout << endl;

}

void Pillars::MoveRing(int from, int to)

{ p[to].Push(p[from].Pop()); }

//............. HANOI.CPP ..........................

#include "PILLAR.H"

void hanoi(Pillars& pillars, int from, int to, int num)

{

if (num > 0)

{

int other = 3 - from - to;

hanoi(pillars, from, other, num - 1);

pillars.MoveRing(from, to);

pillars.Show(); // in order to trace the solution

hanoi(pillars, other, to, num - 1);

}

void main()

{ int n;

cin >> n;

Pillars pillars(n); // first pillar has n rings.

pillars.Show();

hanoi(pillars, 0, 2, n);

}

פלט התוכנית עבור 5 טבעות:

0 Pillar0: ABCDE Pillar1: Pillar2:

1 Pillar0: ABCD Pillar1: Pillar2: E

2 Pillar0: ABC Pillar1: D Pillar2: E

3 Pillar0: ABC Pillar1: DE Pillar2:

4 Pillar0: AB Pillar1: DE Pillar2: C

5 Pillar0: ABE Pillar1: D Pillar2: C

6 Pillar0: ABE Pillar1: Pillar2: CD

7 Pillar0: AB Pillar1: Pillar2: CDE

8 Pillar0: A Pillar1: B Pillar2: CDE

9 Pillar0: A Pillar1: BE Pillar2: CD

10 Pillar0: AD Pillar1: BE Pillar2: C

11 Pillar0: ADE Pillar1: B Pillar2: C

12 Pillar0: ADE Pillar1: BC Pillar2:

13 Pillar0: AD Pillar1: BC Pillar2: E

14 Pillar0: A Pillar1: BCD Pillar2: E

15 Pillar0: A Pillar1: BCDE Pillar2:

16 Pillar0: Pillar1: BCDE Pillar2: A

17 Pillar0: E Pillar1: BCD Pillar2: A

18 Pillar0: E Pillar1: BC Pillar2: AD

19 Pillar0: Pillar1: BC Pillar2: ADE

20 Pillar0: C Pillar1: B Pillar2: ADE

21 Pillar0: C Pillar1: BE Pillar2: AD

22 Pillar0: CD Pillar1: BE Pillar2: A

23 Pillar0: CDE Pillar1: B Pillar2: A

24 Pillar0: CDE Pillar1: Pillar2: AB

25 Pillar0: CD Pillar1: Pillar2: ABE

26 Pillar0: C Pillar1: D Pillar2: ABE

27 Pillar0: C Pillar1: DE Pillar2: AB

28 Pillar0: Pillar1: DE Pillar2: ABC

29 Pillar0: E Pillar1: D Pillar2: ABC

30 Pillar0: E Pillar1: Pillar2: ABCD

31 Pillar0: Pillar1: Pillar2: ABCDE

חישוב רקורסיבי של איברי סדרות Fibonacci ו Lucas

הסדרה של Fibonacci (0, 1, 1, 2, 3, 5, 8, 13, 21 ...) מוגדרת כדלהלן:

הסדרה של Lucas (2, 1, 3, 4, 7, 11, 18, 29, 47 ...) מוגדרת כדלהלן:

שתי תכונות נוספות :

מאפשרות לחשב בצורה רקורסיבית איברים בעלי אינדקס זוגי.

כדי לטפל באיבר בעל אינדקס אי זוגי משתמשים בנוסחאות (1) (2) באופן הבא:

מטרתנו לכתוב פונקצה רקורסיבית לחישוב איבר בסדרת Fibonacci ופונקציה דומה לחישוב איבר בסדרת Lucas.
תנאי העצירה בשתי הפונקציות דומה: אם האידקס של האיבר הוא 0 או 1 אזי הפתרון ידוע.
המקרה הרקורסיבי: כאשר האינדקס של האיבר המבוקש גדול מ 1 אפשר לחשב את האיבר הדרוש באמצעות הפעלת אחת מהנוסחאות הרקורסיביות ((3) (4) (5) (6) ). הנוסחאות (3) ו (4) מתאימות לחישוב רקורסיבי של איברים בעלי אינדקס זוגי. הנוסחאות (5) (6) מתאימות לחישוב רקורסיבי של איברים בעלי אינדקס אי זוגי.
שים לב למקרה של חישוב רקורסיבי של איבר בעל אינדקס זוגי של סידרת Fibonacci. זהו מקרה של רקורסיה משולבת בה בכדי לחשב את האיבר ה 2n בסידרת Fibonacci צריך לחשב את האיבר ה n בסדרת Fibonacci וגם את האיבר ה n בסדרת Lucas.

יעול החישוב הרקורסיבי בשיטת memo-izing:

אפשר לייעל את החישוב הרקורסיבי ע"י שמירת הערכים שכבר חישבנו ולהשתמש בהם במקום לחשבם מחדש.

אנו משתמשים בשני מערכים (של 41 רכיבי long ) לשמירת הערכים המחושבים. את המערכים אנו מאתחלים ב -0ים פרט לשני האברים הראשונים בסדרה, שהם מאותחלים באברי הסדרה המתאימים.

בכל פעם שפונקציה מחשבת איבר חדש בסדרה היא מעדכנת את המערך.

היעול הוא בכך, שפונקציות עוצרות את הרקורסיה כאשר האיבר, בעל האינדקס המבוקש, קיים במערך (הרכיב במערך שונה מאפס).

תנאי העצירה המשופר: אם האינדקס קטן או שווה ל 1 (תנאי העצירה המקורי), או האיבר באינדקס הדרוש, חושב קודם (ערך האיבר המתאים במערך אינו 0), אזי אפשר להחזיר תוצאה מיידית.

//........... FIBLUC.H ....................................

// class for generating elements of Fibonacci and Lucas

// series: Fibonacci: 0, 1, 1, 2, 3, 5, 8, ...

// Lucas: 2, 1, 3, 4, 7, 11, 18, ...

// Uses recursive algorithm for calculating these numbers.

// Stores old results in arrays for faster calculation of new ones.

typedef long elem;

const int TOP = 41;

class FibLucCalc {

public:

FibLucCalc();

elem Fib(int index); // returns the i'th element in Fibonacci

elem Luc(int index); // returns the i'th element in Lucas

void PrintArrays();

private:

elem fibon[TOP];

elem lucas[TOP];

};

//........... FIBLUC.CPP ....................................

#include <iostream.h>

#include <iomanip.h>

#include "FIBLUC.H"

FibLucCalc::FibLucCalc()

{

fibon[0] = 0; // 0, 1, ...

fibon[1] = 1;

lucas[0] = 2; // 2, 1, ...

lucas[1] = 1;

for (int i = 2; i < TOP; i++) // 0's in both arrays

fibon[i] = lucas[i] = 0;

}

elem FibLucCalc::Luc(int index)

{

if (index < 2) // stopping condition.

return lucas[index];

if (lucas[index]) // if element was calculated before

return lucas[index];

if (index % 2)

return lucas[index] = Luc(index+1) - Luc(index-1);

int h = index / 2;

elem f = h % 2 ? -2 : 2; // (-1)^n * 2

elem g = Luc(h);

return lucas[index] = g * g - f;

}

elem FibLucCalc::Fib(int index)

{

if (index < 2) // stopping condition.

return fibon[index];

if (fibon[index]) // if element was calculated before

return fibon[index];

if (index % 2)

return fibon[index] = Fib(index+1) - Fib(index-1);

int h = index / 2;

return

fibon[index] = Fib(h) * Luc(h);

}

// Printing the content of the arrays 5 numbers in a row.

void FibLucCalc::PrintArrays()

{

int i;

cout << "\nFibonacci calculated values:" << endl;

for (i = 1; i <= TOP; i++)

cout << setw(11) << fibon[i-1] << (i % 5 ? ' ' : '\n');

cout << "\nLucas calculated values:" << endl;

for (i = 1; i <= TOP; i++)

cout << setw(11) << lucas[i-1] << (i % 5 ? ' ' : '\n');

cout << endl;

}

//........... USE.CPP

#include "FIBLUC.H"

void main()

{

int index;

char c;

FibLucCalc fl;

cout << "Type F for Fibonacci, or L for Lucas, ";

cout << "then the index of the number you want (Q to quit):\n";

while (cin >> c >> index, c != 'Q')

{

if (c == 'F')

cout << "Fibon" << index << ": " << fl.Fib(index) << endl;

else if ( c == 'L')

cout << "Lucas" << index << ": " << fl.Luc(index) << endl;

}

g.PrintArrays();

}

חזרה להתחלה